Advertisements
Advertisements
प्रश्न
In Fig. 7, two equal circles, with centres O and O’, touch each other at X. OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with centre O, at the point C. O’D is perpendicular to AC. Find the value of `(DO')/(CO')`

उत्तर
AO’ = O’X = XO = OC …..(Since the two circles are equal.)
So, OA = AO’ + O’X + XO …..(A-O’-X-O)
∴ OA = 3O’A
In ΔAO'D and ΔAOC,
∠DAO'= ∠CAO ....(Common angle)
∠ADO'= ∠ACO ....(both measure 90°)
∴ ΔADO' ~ ΔACO ....(By AA test of similarity)
`:.(DO')/(CO')=(O'A)/(OA)=(O'A)/(3O'A)=1/3`
संबंधित प्रश्न
A tangent to a circle intersects it in ______ point (s).
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA.
Show that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
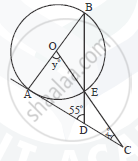
In the given figure AC is a tangent to the circle with centre O.
If ∠ADB = 55° , find x and y. Give reasons for your answers.
Find the length of the tangent from a point which is at a distance of 5cm from the centre of the circle of radius 3cm.
If Δ PQR is isosceles with PQ = PR and a circle with centre O and radius r is the incircle of the Δ PQR touching QR at T, prove that the point T bisects QR.
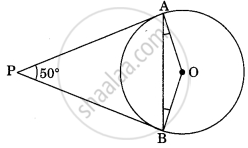
In the figure, if PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠OAB is equal to ______.
In the given figure, PA is a tangent to the circle drawn from the external point P and PBC is the secant to the circle with BC as diameter. If ∠AOC = 130°, then find the measure of ∠APB, where O is the centre of the circle.

A circle of radius 5.2 cm has two tangents AB and CD parallel to each other. What is the distance between the two tangents?
In the given diagram an isosceles ΔABC is inscribed in a circle with centre O. PQ is a tangent to the circle at C. OM is perpendicular to chord AC and ∠COM = 65°.

Find:
- ∠ABC
- ∠BAC
- ∠BCQ
