Advertisements
Advertisements
प्रश्न
Show that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
उत्तर
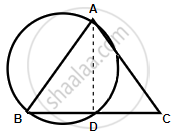
Join AD.
AB is the diameter.
∴ ∠ADB = 90° ...(Angle in a semi-circle)
But, ∠ADB + ∠ADC = 180° ...(Linear pair)
`=>` ∠ADC = 90°
In ΔABD and ΔACD,
∠ADB = ∠ADC ...(Each 90°)
AB = AC ...(Given)
AD = AD ...(Common)
ΔABD ≅ ΔACD ...(RHS congruence criterion)
`=>` BD = DC ...(C.P.C.T)
Hence, the circle bisects base BC at D.
APPEARS IN
संबंधित प्रश्न
A circle can have ______ parallel tangents at the most.
In the given figure, find TP if AT = 16 cm and AB = 12 cm.

In Fig.2, a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively, If AB = 29 cm, AD = 23 cm, ∠B = 90° and DS = 5 cm, then the radius of the circle (in cm.) is:
AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°. The tangent at C intersects extended AB at a point D. Prove that BC = BD.
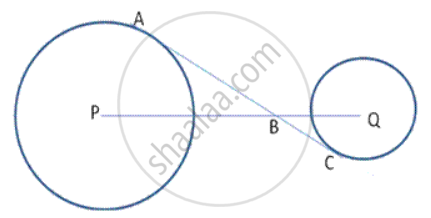
In the following fig. , AC is a transversal common tangent to tvvo circles with centres P and Q and of radii 6cm and 3cm respectively. Given that AB = 8cm, calculate PQ.
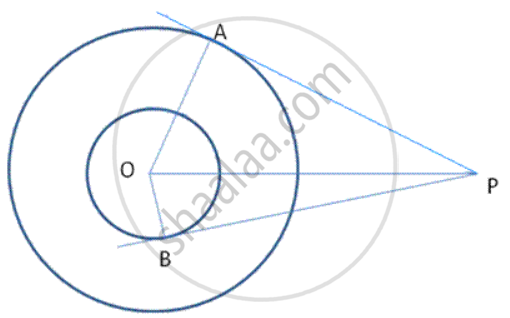
In followinf fig., two concentric circles with centre 0 are of radii 5 cm and 3 cm. from an external point P, tangents PA and PB are drawn to these circles. If AP = 12cm, find BP.
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find the length of tangent PT.

In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle AOB

In the figure given below, PT is a tangent to the circle. Find PT if AT = 16 cm and AB = 12 cm.
In the given figure O, is the centre of the circle. CE is a tangent to the circle at A. If ∠ABD = 26° find:
- ∠BDA
- ∠BAD
- ∠CAD
- ∠ODB

