Advertisements
Advertisements
प्रश्न
AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°. The tangent at C intersects extended AB at a point D. Prove that BC = BD.
उत्तर
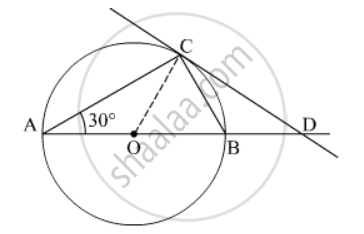
It is given that ∠BAC = 30° and AB is diameter.
∠ACB = 90° ...(Angle formed by the diameter is 90°)
In ∆ABC,
∠ACB + ∠BAC + ∠ABC = 180°
⇒ 90° + 30° + ∠ABC = 180°
⇒ ∠ABC = 60°
⇒ ∠CBD = 180° – 60° = 120° ...(∠CBD and ∠ABC form a linear pair)
In ∆OCD,
∠OCD = 90° ...(Angle made by Radius on the tangent)
∠OBC = ∠ABC = 60°
Since OB = OC,
∠OCB = ∠OBC = 60° ...(OC = OB = radius)
In ∆OCB,
⇒ ∠COB + ∠OCB + ∠OBC = 180°
⇒ ∠COB + 60° + 60° = 180°
⇒ ∠COB = 60°
In ∆OCD,
∠COD + ∠OCD + ∠ODC = 180°
⇒ 60° + 90° + ∠ODC = 90° ...(∠COD = ∠COB)
⇒ ∠ODC = 30°
In ∆CBD,
∠CBD = 120°
∠BDC = ∠ODC = 30°
⇒ ∠BCD + ∠BDC + ∠CBD = 180°
⇒ ∠BCD + 30° + 120° = 180°
⇒ ∠BCD + 30° = ∠BDC
Angles made by BC and BD on CD are equal, so ∆CBD is an isosceles triangle and therefore, BC = BD.
संबंधित प्रश्न
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA.
In triangle PQR, PQ = 24 cm, QR = –7 cm and ∠PQR = 90°. Find the radius of the inscribed circle.

In Figure 2, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA + AR = XB + BR ?

From a point Q, 13 cm away from the centre of a circle, the length of tangent PQ to the circle is 12 cm. The radius of the circle (in cm) is
Four alternative answers for the following question is given. Choose the correct alternative.
If two circles are touching externally, how many common tangents of them can be drawn?
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
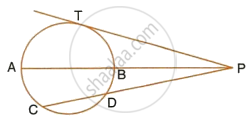
In the following figure, seg AB is the diameter of the circle with center P. Line CB be the tangent and line AC intersects a circle in point D. Prove that:
AC x AD = 4 (radius)2

In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find:
- AB.
- the length of tangent PT.
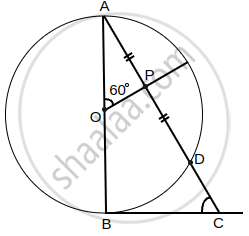
In the given figure, AB is diameter of a circle centered at O. BC is tangent to the circle at B. If OP bisects the chord AD and ∠AOP = 60°, then find ∠C.
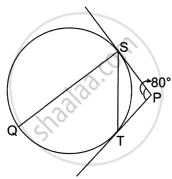
In the given diagram, PS and PT are the tangents to the circle. SQ || PT and ∠SPT = 80°. The value of ∠QST is ______.