Advertisements
Advertisements
प्रश्न
In the following figure, seg AB is the diameter of the circle with center P. Line CB be the tangent and line AC intersects a circle in point D. Prove that:
AC x AD = 4 (radius)2

उत्तर
Given: A circle with center P. CB tangent and line AC intersect a circle in point D
Construction: Join BD.
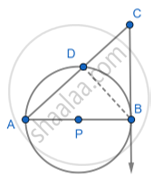
To Prove: ∴ ∠ADB =90° [Angle inscribed in semicircle]
∴ ∠PBC = 90° [Tangent perpendicular to the radius]
i.e. ∠ABC =90°
In Δ ACB and Δ ABD
∠ ABC = ∠ ADB [Each is of 90°]
∴ ∠ CAB = ∠DAB [Common angle]
∴ ΔACB ∼ ΔABD [AA property]
∴ `"AC"/"AB"="AB"/"AD"`
∴AC × AD = (AB)2…(1)
AP = PB …(radii of the same circle)
∴ AB = AP +PB
∴ AB = 2AP
Substituting the value of AB in equation (1)
AC × AD = (2AP)2
∴ AC × AD = 4(AP)2
∴ AC × AD =4 (radius)2
APPEARS IN
संबंधित प्रश्न
How many tangents can a circle have?
A line intersecting a circle in two points is called a ______.
A circle can have ______ parallel tangents at the most.
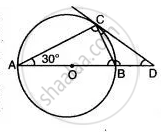
In the given figure O is the centre of the circle. Tangents A and B meet at C. If ∠ACO = 30°, find
1) ∠BCO
2) ∠AOB
3) ∠APB
The given figure shows a circle with centre O and BCD is tangent to it at C. Show that : ∠ACD + ∠BAC = 90°.

In Figure 3, a right triangle ABC, circumscribes a circle of radius r. If AB and BC are of lengths of 8 cm and 6 cm respectively, find the value of r.

In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (ii) radius of the circle.

PA and PB are tangents from P to the circle with centre O. At M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
In following figure , the incircle of Δ ABC , touches the sides BC , CA and AB at D , E and F respectively. Show AF + BD + CE = AE + BF + CD
Find the area of sector whose central angle and radius are 60o and 21 cm respectively.
`(pi = 22/7)`
In Figure, AB is diameter and AC is a chord of a circle such that ∠BAC = 30°. The tangent at C intersects AB produced at D. Prove that BC = BD.
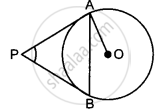
If PA and PB are two tangents drawn from a point P to a circle with center C touching it A and B, prove that CP is the perpendicular bisector of AB.
In the figure PA and PB are tangents to the circle with centre O. If ∠APB = 60°, then ∠OAB is ______
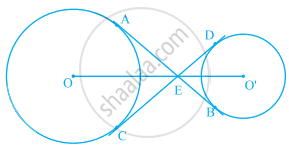
In figure, the common tangent, AB and CD to two circles with centres O and O' intersect at E. Prove that the points O, E, O' are collinear.
In figure, O is the centre of a circle of radius 5 cm, T is a point such that OT = 13 cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find the length of AB.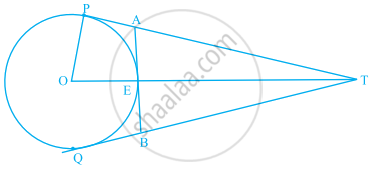
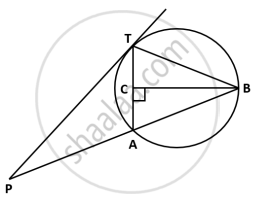
In the given figure, PT is a tangent to the circle at T, chord BA is produced to meet the tangent at P. Perpendicular BC bisects the chord TA at C. If PA = 9 cm and TB = 7 cm, find the lengths of:
- AB
- PT
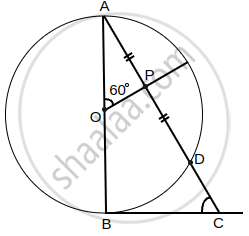
In the given figure, AB is diameter of a circle centered at O. BC is tangent to the circle at B. If OP bisects the chord AD and ∠AOP = 60°, then find ∠C.
In the given figure, XAY is a tangent to the circle centered at O. If ∠ABO = 40°, then find ∠BAY and ∠AOB.

