Advertisements
Advertisements
प्रश्न
In the given figure O is the centre of the circle. Tangents A and B meet at C. If ∠ACO = 30°, find
1) ∠BCO
2) ∠AOB
3) ∠APB
उत्तर
In ΔAOC, ACO = 30° (Given)

∠OAC = 90° [radius is perpendicular to the tangent at the point of contact]
By angle sum property, ACO + OAC + AOC = 180o
AOC = 180° – (90° + 30°) = 60°
Consider Δ AOC and Δ BOC
AO = BO (radii)
AC = BC (tangents to a circle from an external point are equal in length)
OC = OC (Common)
ΔAOC ≅ ΔBOC
1) ∠BCO = ∠ACO = 30°
2) ∠AOC = ∠BOC = 60°
∠AOB = ∠AOC + ∠BOC = 120°
3) We know that, “If two angles stand on the same chord, then the angle at the centre is twice the angle at the circumference.
∠AOB and ∠APB stand on the same chord AB.
∠AOB = 2∠APB
So ∠APB = 1/2 ∠AOB = 60°
APPEARS IN
संबंधित प्रश्न
In Fig. 1, PQ is a tangent at a point C to a circle with centre O. if AB is a diameter and ∠CAB = 30°, find ∠PCA.

In triangle PQR, PQ = 24 cm, QR = –7 cm and ∠PQR = 90°. Find the radius of the inscribed circle.

The given figure shows a circle with centre O and BCD is tangent to it at C. Show that : ∠ACD + ∠BAC = 90°.

In Fig. 1, AOB is a diameter of a circle with centre O and AC is a tangent to the circle at A. If ∠BOC = 130°, the find ∠ACO.

Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
In fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PB = 9cm and AB = 5 cm, find PT.
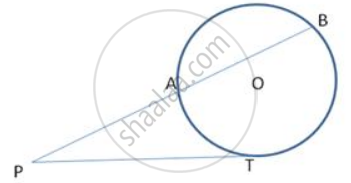
In following fig., ABC is a right- angled triangle at A with sides AB = 5 cm and BC = 13 cm . A circle with centre O has been inscribed in the triangle ABC. Calculate the radius of the incircle.
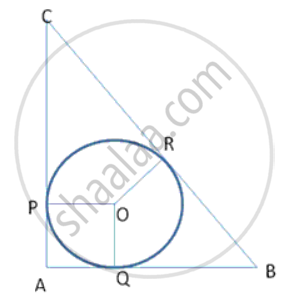
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find the length of tangent PT.

In figure, M is the centre of the circle and seg KL is a tangent segment. If MK = 12, KL = `6sqrt(3)`, then find
(i) Radius of the circle.
(ii) Measures of ∠K and ∠M.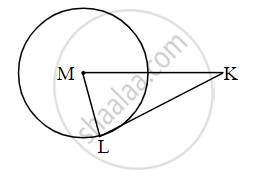
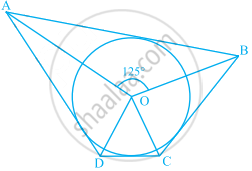
In figure, if ∠AOB = 125°, then ∠COD is equal to ______.