Advertisements
Advertisements
प्रश्न
In figure, M is the centre of the circle and seg KL is a tangent segment. If MK = 12, KL = `6sqrt(3)`, then find
(i) Radius of the circle.
(ii) Measures of ∠K and ∠M.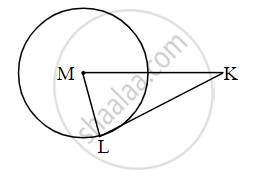
उत्तर
(i)
Line KL is the tangent to the circle at point L and seg ML is the radius. ......[Given]
∴ ∠MLK = 90° ......(i) [Tangent theorem]
In ∆MLK,
∠MLK = 90°
∴ MK2 = ML2 + KL2 .....[Pythagoras theorem]
∴ 122 = ML2 + `(6sqrt(3))^2`
∴ 144 = ML2 + 108
∴ ML2 = 144 − 108
∴ ML2 = 36
∴ ML = `sqrt(36)`
∴ ML = 6 units ......[Taking square root of both sides]
∴ Radius of the circle is 6 units.
(ii)
We know that,
ML = `1/2` MK,
∴ ∠K = 30° .....(ii) [Converse of 30°−60°−90° theorem]
In ∆MLK,
∠L = 90° .....[From (i)]
∠K = 30° .....[From (ii)]
∴ ∠M = 60° ......[Remaining angle of ∆MLK]
APPEARS IN
संबंधित प्रश्न
If the angle between two tangents drawn from an external point P to a circle of radius a and centre O, is 60°, then find the length of OP
In the given figure O is the centre of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm. Calculate the radius of a circle.

In the given figure, find TP if AT = 16 cm and AB = 12 cm.

In Figure 2, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA + AR = XB + BR ?

In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (ii) radius of the circle.

In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
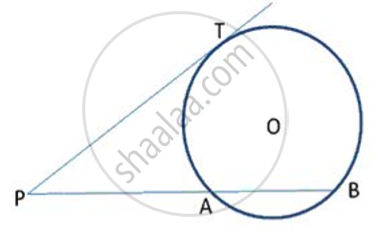
If Δ PQR is isosceles with PQ = PR and a circle with centre O and radius r is the incircle of the Δ PQR touching QR at T, prove that the point T bisects QR.
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate ∠ PAD.

In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle AOB

Construct a tangent to a circle with centre O and radius 3.5 cm at a point P on it.
At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance 8 cm from A is ______
In figure, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°. Then AT is equal to ______.

Two parallel lines touch the circle at
points A and B respectively. If the area of the circle is 25 n cm2, then AB is equal to ______
In the figure PA and PB are tangents to the circle with centre O. If ∠APB = 60°, then ∠OAB is ______
ABCD is a cyclic quadrilateral PQ is a tangent at B. If ∠DBQ = 65°, then ∠BCD is ______

If two tangents TL and TM are drawn to a circle with centre C such that ∠LTM = 70°, then find ∠MCT.
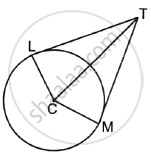
A tangent JK is drawn to a circle with centre C such that CK = 6 cm and ∠CKJ = 60°. Find the length of the tangent JK.

In the given figure, XAY is a tangent to the circle centered at O. If ∠ABO = 40°, then find ∠BAY and ∠AOB.

In the adjoining figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 30°, find the value of x.

