Advertisements
Advertisements
प्रश्न
A tangent JK is drawn to a circle with centre C such that CK = 6 cm and ∠CKJ = 60°. Find the length of the tangent JK.

उत्तर
JK is a tangent at the point J and CJ is a radius.
So, CK = 6 cm and ∠CKJ = 60° ......[Given]
Now, ∠CKJ = 90° ......[Tangent theorem]
In ΔCJK,

cos 60° = `"Base"/"Hypotenuse"`
⇒ cos 60° = `(JK)/(KC) = (JK)/6`
⇒ `1/2 = (JK)/6`
⇒ JK = 3
Hence, the length of JK is 3 cm.
APPEARS IN
संबंधित प्रश्न
In the figure given below, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT = 60°, find ∠PRQ.

A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is ______.
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD
Show that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
In Fig. 1, AOB is a diameter of a circle with centre O and AC is a tangent to the circle at A. If ∠BOC = 130°, the find ∠ACO.


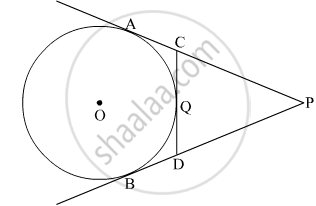
In the figure, point Q is the
point of contact. If PQ = 12,
PR = 8 then find PS.
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (ii) radius of the circle.

In the given figure AC is a tangent to the circle with centre O.
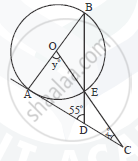
If ∠ADB = 55° , find x and y. Give reasons for your answers.
Find the length of the tangent from a point which is at a distance of 5cm from the centre of the circle of radius 3cm.
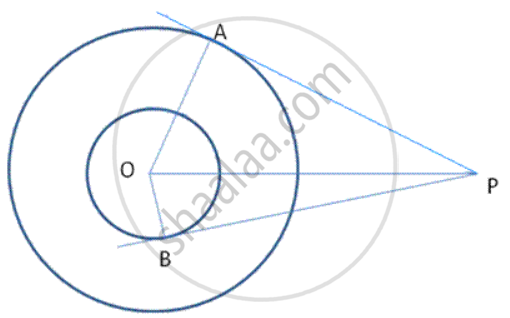
In followinf fig., two concentric circles with centre 0 are of radii 5 cm and 3 cm. from an external point P, tangents PA and PB are drawn to these circles. If AP = 12cm, find BP.
If Δ PQR is isosceles with PQ = PR and a circle with centre O and radius r is the incircle of the Δ PQR touching QR at T, prove that the point T bisects QR.
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find AB.

Find the area of sector whose central angle and radius are 60o and 21 cm respectively.
`(pi = 22/7)`
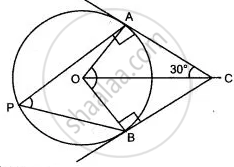
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO = 30°,
find: (i) ∠ BCO (ii) ∠ AOB (iii) ∠ APB
ABCD is a cyclic quadrilateral PQ is a tangent at B. If ∠DBQ = 65°, then ∠BCD is ______

Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.
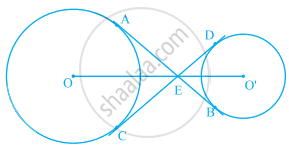
In figure, the common tangent, AB and CD to two circles with centres O and O' intersect at E. Prove that the points O, E, O' are collinear.
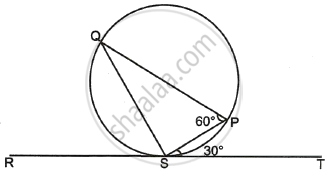
In the given diagram RT is a tangent touching the circle at S. If ∠PST = 30° and ∠SPQ = 60°, then ∠PSQ is equal to ______.
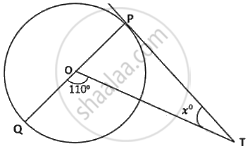
In the adjoining diagram, O is the centre of the circle and PT is a tangent. The value of x is ______.