Advertisements
Advertisements
प्रश्न
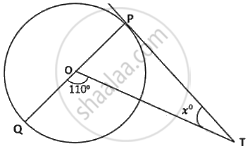
In the adjoining diagram, O is the centre of the circle and PT is a tangent. The value of x is ______.
विकल्प
20°
40°
55°
70°
उत्तर
In the adjoining diagram, O is the centre of the circle and PT is a tangent. The value of x is 20°.
Explanation:
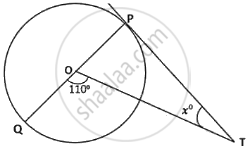
Given:
- O is the center of the circle.
- PT is a tangent to the circle at point T.
When a tangent and a radius intersect at the point of tangency, the angle formed between the radius and the tangent is 90°. This is a key property of circles and tangents.
Let's analyze the situation step by step:
Step-by-Step Solution
1. Identify the key points and angles:
- O is the center.
- PT is the tangent.
- OT is the radius.
- ∠OTP = 90° because the radius and tangent are perpendicular at the point of tangency.
2. Determine the relationship involving z:
Suppose we have a triangle OTP, where T is the point of tangency. Let's consider an angle ∠OTP which is 90°, and we are given that x = 20°.
3. Use the properties of the right triangle:
Since ∠OTP = 90°, we can identify other angles in the triangle.
If there is another angle related to a in this problem, let's denote it as ∠TOP.
Assuming x is a part of the complementary angle
Let's assume x is related to ∠OTP.
- ∠OTP + ∠PTO + ∠TOP = 180° ...(Sum of angles in a triangle)
- Given ∠OTP = 90°, we have:
90° + ∠PTO + x = 180° - Simplifying:
∠PTO + x = 90° - Given x = 20°:
∠PTO + 20° = 90°
∠PTO + 70°
So, the given value x = 20° complements ∠PTO which results in a 70° angle to satisfy the conditions of the right triangle formed by the tangent and radius.
APPEARS IN
संबंधित प्रश्न
In the figure given below, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT = 60°, find ∠PRQ.

In Fig. 1, PQ is a tangent at a point C to a circle with centre O. if AB is a diameter and ∠CAB = 30°, find ∠PCA.

A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA.
In Figure 1, AP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC
= 4 cm, then the length of AP (in cm) is
In the adjoining figure the radius of a circle with centre C is 6 cm, line AB is a tangent at A. Answer the following questions.
(1) What is the measure of ∠CAB ? Why ?
(2) What is the distance of point C from line AB? Why ?
(3) d(A,B) = 6 cm, find d(B,C).
(4) What is the measure of ∠ABC ? Why ? 
Draw Δ ABC such that, AB = 8 cm, BC = 6 cm and ∠ B = 90°. Draw seg BD
perpendicular to hypotenuse AC. Draw a circle passing through points
B, D, A. Show that line CB is a tangent of the circle.
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
A point A is 17cm from the centre of the circle. The length of the tangent drawn from A to the circle is 15cm. find the radius of the circle.
ABC is a right triangle with angle B = 90º. A circle with BC as diameter meets by hypotenuse AC at point D. Prove that: BD2 = AD × DC.
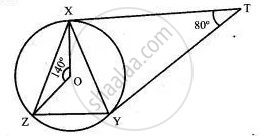
In the alongside, figure, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°. Calculate the value of ∠ZXY.