Advertisements
Advertisements
प्रश्न
In the adjoining figure the radius of a circle with centre C is 6 cm, line AB is a tangent at A. Answer the following questions.
(1) What is the measure of ∠CAB ? Why ?
(2) What is the distance of point C from line AB? Why ?
(3) d(A,B) = 6 cm, find d(B,C).
(4) What is the measure of ∠ABC ? Why ? 
उत्तर
(1) It is given that line AB is tangent to the circle at A.
∴ ∠CAB = 90º (Tangent at any point of a circle is perpendicular to the radius throught the point of contact)
Thus, the measure of ∠CAB is 90º. 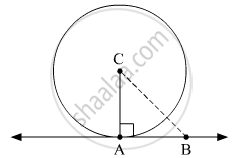
(2) Distance of point C from AB = 6 cm (Radius of the circle)
(3) ∆ABC is a right triangle.
CA = 6 cm and AB = 6 cm
Using Pythagoras theorem, we have
\[{BC}^2 = {AB}^2 + {CA}^2 \]
\[ \Rightarrow BC = \sqrt{6^2 + 6^2} \]
\[ \Rightarrow BC = 6\sqrt{2} cm\]
Thus, d(B, C) = \[6\sqrt{2}\]
(4) In right ∆ABC, AB = CA = 6 cm
∴ ∠ACB = ∠ABC (Equal sides have equal angles opposite to them)
Also, ∠ACB + ∠ABC = 90º (Using angle sum property of triangle)
∴ 2∠ABC = 90º
⇒ ∠ABC = \[\frac{90^\circ}{2}\]
Thus, the measure of ∠ABC is 45º.
APPEARS IN
संबंधित प्रश्न
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
The given figure shows a circle with centre O and BCD is tangent to it at C. Show that : ∠ACD + ∠BAC = 90°.

In Fig. 1, AOB is a diameter of a circle with centre O and AC is a tangent to the circle at A. If ∠BOC = 130°, the find ∠ACO.

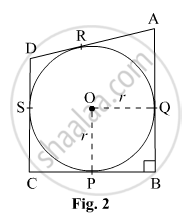
In Fig.2, a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively, If AB = 29 cm, AD = 23 cm, ∠B = 90° and DS = 5 cm, then the radius of the circle (in cm.) is:
What is the distance between two parallel tangents of a circle having radius 4.5 cm ? Justify your answer.
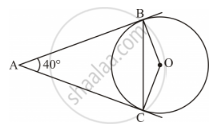
In the given Figure, AB and AC are tangents to the circle with centre O such that ∠BAC = 40°. Then ∠BOC is equal to ______
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (ii) radius of the circle.

A point A is 17cm from the centre of the circle. The length of the tangent drawn from A to the circle is 15cm. find the radius of the circle.
PA and PB are tangents from P to the circle with centre O. At M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ∠ BAM = ∠ BMA
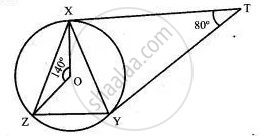
In the alongside, figure, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°. Calculate the value of ∠ZXY.
In the figure PA and PB are tangents to the circle with centre O. If ∠APB = 60°, then ∠OAB is ______
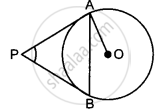
In the following figure, PA and PB are tangents from a point P to a circle with centre O. Then the quadrilateral OAPB must be a ______

Find the value of ∠DCE.

Construct a pair of tangents to a circle of radius 4 cm, which are inclined to each other at an angle of 60°.
In the given figure, AB is diameter of a circle centered at O. BC is tangent to the circle at B. If OP bisects the chord AD and ∠AOP = 60°, then find ∠C.
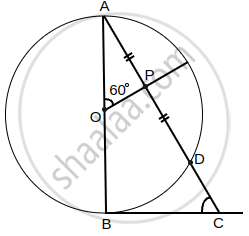
In the adjoining figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 30°, find the value of x.

In the given figure O, is the centre of the circle. CE is a tangent to the circle at A. If ∠ABD = 26° find:
- ∠BDA
- ∠BAD
- ∠CAD
- ∠ODB

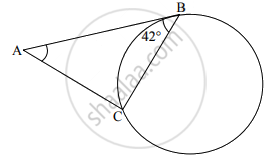
In the given figure, AB and AC are tangents to the circle. If ∠ABC = 42°, then the measure of ∠BAC is ______.
