Advertisements
Advertisements
Question
In the adjoining figure the radius of a circle with centre C is 6 cm, line AB is a tangent at A. Answer the following questions.
(1) What is the measure of ∠CAB ? Why ?
(2) What is the distance of point C from line AB? Why ?
(3) d(A,B) = 6 cm, find d(B,C).
(4) What is the measure of ∠ABC ? Why ? 
Solution
(1) It is given that line AB is tangent to the circle at A.
∴ ∠CAB = 90º (Tangent at any point of a circle is perpendicular to the radius throught the point of contact)
Thus, the measure of ∠CAB is 90º. 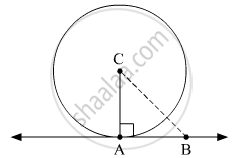
(2) Distance of point C from AB = 6 cm (Radius of the circle)
(3) ∆ABC is a right triangle.
CA = 6 cm and AB = 6 cm
Using Pythagoras theorem, we have
\[{BC}^2 = {AB}^2 + {CA}^2 \]
\[ \Rightarrow BC = \sqrt{6^2 + 6^2} \]
\[ \Rightarrow BC = 6\sqrt{2} cm\]
Thus, d(B, C) = \[6\sqrt{2}\]
(4) In right ∆ABC, AB = CA = 6 cm
∴ ∠ACB = ∠ABC (Equal sides have equal angles opposite to them)
Also, ∠ACB + ∠ABC = 90º (Using angle sum property of triangle)
∴ 2∠ABC = 90º
⇒ ∠ABC = \[\frac{90^\circ}{2}\]
Thus, the measure of ∠ABC is 45º.
APPEARS IN
RELATED QUESTIONS
In Fig. 7, two equal circles, with centres O and O’, touch each other at X. OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with centre O, at the point C. O’D is perpendicular to AC. Find the value of `(DO')/(CO')`

How many common tangents can be drawn to two circles, touching each
other externally?
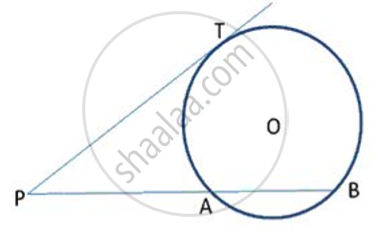
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
A point A is 17cm from the centre of the circle. The length of the tangent drawn from A to the circle is 15cm. find the radius of the circle.
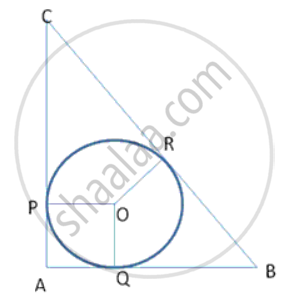
In following fig., ABC is a right- angled triangle at A with sides AB = 5 cm and BC = 13 cm . A circle with centre O has been inscribed in the triangle ABC. Calculate the radius of the incircle.
If Δ PQR is isosceles with PQ = PR and a circle with centre O and radius r is the incircle of the Δ PQR touching QR at T, prove that the point T bisects QR.
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find the length of tangent PT.

ABC is a right triangle with angle B = 90º. A circle with BC as diameter meets by hypotenuse AC at point D. Prove that: BD2 = AD × DC.
In the following figure, seg AB is the diameter of the circle with center P. Line CB be the tangent and line AC intersects a circle in point D. Prove that:
AC x AD = 4 (radius)2

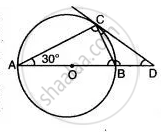
In Figure, AB is diameter and AC is a chord of a circle such that ∠BAC = 30°. The tangent at C intersects AB produced at D. Prove that BC = BD.
In Fig. TA is a tangent to a circle from the point T and TBC is a secant to the circle. If AD is the bisector of ∠BAC, prove that ΔADT is isosceles.

In the figure, if PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠OAB is equal to ______.
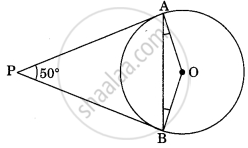
In the following figure, PA and PB are tangents from a point P to a circle with centre O. Then the quadrilateral OAPB must be a ______

ABCD is a cyclic quadrilateral PQ is a tangent at B. If ∠DBQ = 65°, then ∠BCD is ______

Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.
In figure, O is the centre of a circle of radius 5 cm, T is a point such that OT = 13 cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find the length of AB.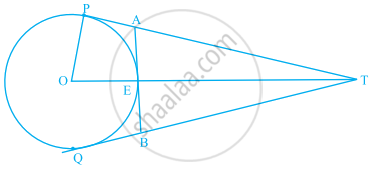
In the given figure, XAY is a tangent to the circle centered at O. If ∠ABO = 40°, then find ∠BAY and ∠AOB.

ΔABC circumscribes a circle of radius r such that ∠B = 90°. If AB = 3 cm and BC = 4 cm, then find the value of r.
The distance between two tangents parallel to each other of a circle is 13 cm. Find the radius of the circle.
In the given diagram an isosceles ΔABC is inscribed in a circle with centre O. PQ is a tangent to the circle at C. OM is perpendicular to chord AC and ∠COM = 65°.

Find:
- ∠ABC
- ∠BAC
- ∠BCQ
