Advertisements
Advertisements
Question
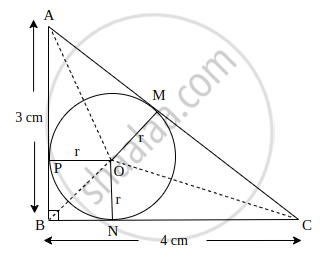
ΔABC circumscribes a circle of radius r such that ∠B = 90°. If AB = 3 cm and BC = 4 cm, then find the value of r.
Solution
Here, AB, BC and CA are the tangents to the circle at P, N and M, respectively.
Also, OP = ON = OM = r ...(Radius of the circle)
Area of ΔABC = `1/2` × BC × AB
= `1/2 xx 4 xx 3` ...[∵ Area of Δ = `1/2` × base × height]
= 6 sq. cm
Now, using pythogoras in right ΔABC, we get
CA2 = AB2 + BC2
⇒ CA2 = (3)2 + (4)2
⇒ CA2 = 9 + 16
⇒ CA2 = 25
⇒ CA = 5 cm
Now, Area of ΔABC = Area of ΔOAB + area of ΔOBC + Area of ΔOCA
⇒ 6 = `1/2 xx r xx "AB" + 1/2 xx r xx "BC" + 1/2 xx r xx "CA"`
⇒ 6 = `1/2 xx r("AB" + "BC" + "CA")`
⇒ 12 = r(3 + 4 + 5)
⇒ 12 = 12r
⇒ r = 1 cm
APPEARS IN
RELATED QUESTIONS
How many tangents can a circle have?
In Figure 1, AP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC
= 4 cm, then the length of AP (in cm) is
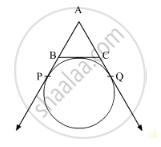
PA and PB are tangents from P to the circle with centre O. At M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
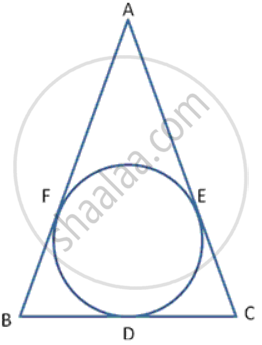
In following figure , the incircle of Δ ABC , touches the sides BC , CA and AB at D , E and F respectively. Show AF + BD + CE = AE + BF + CD
In the following figure, seg AB is the diameter of the circle with center P. Line CB be the tangent and line AC intersects a circle in point D. Prove that:
AC x AD = 4 (radius)2

Two circle with radii r1 and r2 touch each other externally. Let r be the radius of a circle which touches these two circle as well as a common tangent to the two circles, Prove that: `1/sqrtr + 1/sqrtr_1 + 1/sqrtr_2`.
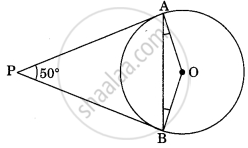
In the figure, if PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠OAB is equal to ______.
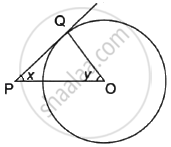
In the given figure, PQ is a tangent to the circle with centre O. If ∠OPQ = x, ∠POQ = y, then x + y is ______.

In the given figure, QR is a common tangent to the two given circles touching externally at A. The tangent at A meets QR at P. If AP = 4.2 cm, then the length of QR is ______.
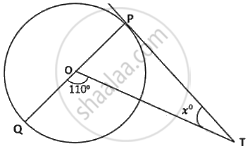
In the adjoining diagram, O is the centre of the circle and PT is a tangent. The value of x is ______.