Advertisements
Advertisements
प्रश्न
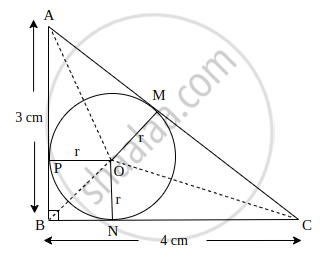
ΔABC circumscribes a circle of radius r such that ∠B = 90°. If AB = 3 cm and BC = 4 cm, then find the value of r.
उत्तर
Here, AB, BC and CA are the tangents to the circle at P, N and M, respectively.
Also, OP = ON = OM = r ...(Radius of the circle)
Area of ΔABC = `1/2` × BC × AB
= `1/2 xx 4 xx 3` ...[∵ Area of Δ = `1/2` × base × height]
= 6 sq. cm
Now, using pythogoras in right ΔABC, we get
CA2 = AB2 + BC2
⇒ CA2 = (3)2 + (4)2
⇒ CA2 = 9 + 16
⇒ CA2 = 25
⇒ CA = 5 cm
Now, Area of ΔABC = Area of ΔOAB + area of ΔOBC + Area of ΔOCA
⇒ 6 = `1/2 xx r xx "AB" + 1/2 xx r xx "BC" + 1/2 xx r xx "CA"`
⇒ 6 = `1/2 xx r("AB" + "BC" + "CA")`
⇒ 12 = r(3 + 4 + 5)
⇒ 12 = 12r
⇒ r = 1 cm
APPEARS IN
संबंधित प्रश्न
How many tangents can a circle have?
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is ______.
What is the distance between two parallel tangents of a circle having radius 4.5 cm ? Justify your answer.
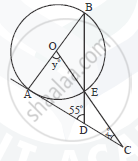
In the given figure AC is a tangent to the circle with centre O.
If ∠ADB = 55° , find x and y. Give reasons for your answers.
A chord of a length 16.8 cm is at a distance of 11.2 cm from the centre of a circle . Find the length of the chord of the same circle which is at a distance of 8.4 cm from the centre.
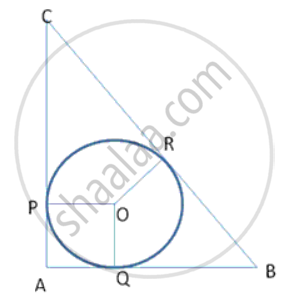
In following fig., ABC is a right- angled triangle at A with sides AB = 5 cm and BC = 13 cm . A circle with centre O has been inscribed in the triangle ABC. Calculate the radius of the incircle.
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle AOB

In Question 5 above, if radii of the two circles are equal, prove that AB = CD.
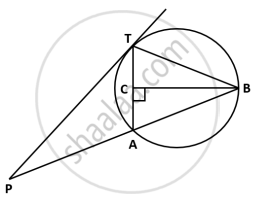
In the given figure, PT is a tangent to the circle at T, chord BA is produced to meet the tangent at P. Perpendicular BC bisects the chord TA at C. If PA = 9 cm and TB = 7 cm, find the lengths of:
- AB
- PT
In the given figure, XAY is a tangent to the circle centered at O. If ∠ABO = 40°, then find ∠BAY and ∠AOB.

