Advertisements
Advertisements
प्रश्न
ΔABC circumscribes a circle of radius r such that ∠B = 90°. If AB = 3 cm and BC = 4 cm, then find the value of r.
उत्तर
Here, AB, BC and CA are the tangents to the circle at P, N and M, respectively.
Also, OP = ON = OM = r ...(Radius of the circle)
Area of ΔABC = `1/2` × BC × AB
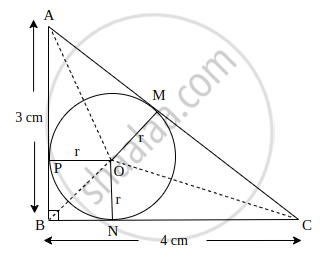
= `1/2 xx 4 xx 3` ...[∵ Area of Δ = `1/2` × base × height]
= 6 sq. cm
Now, using pythogoras in right ΔABC, we get
CA2 = AB2 + BC2
⇒ CA2 = (3)2 + (4)2
⇒ CA2 = 9 + 16
⇒ CA2 = 25
⇒ CA = 5 cm
Now, Area of ΔABC = Area of ΔOAB + area of ΔOBC + Area of ΔOCA
⇒ 6 = `1/2 xx r xx "AB" + 1/2 xx r xx "BC" + 1/2 xx r xx "CA"`
⇒ 6 = `1/2 xx r("AB" + "BC" + "CA")`
⇒ 12 = r(3 + 4 + 5)
⇒ 12 = 12r
⇒ r = 1 cm
APPEARS IN
संबंधित प्रश्न
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
If the angle between two tangents drawn from an external point P to a circle of radius a and centre O, is 60°, then find the length of OP
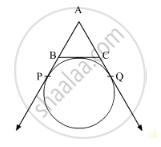
In Figure 1, AP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC
= 4 cm, then the length of AP (in cm) is
What is the distance between two parallel tangents of a circle having radius 4.5 cm ? Justify your answer.
Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle.
In the following figure, seg AB is the diameter of the circle with center P. Line CB be the tangent and line AC intersects a circle in point D. Prove that:
AC x AD = 4 (radius)2

In figure, M is the centre of the circle and seg KL is a tangent segment. If MK = 12, KL = `6sqrt(3)`, then find
(i) Radius of the circle.
(ii) Measures of ∠K and ∠M.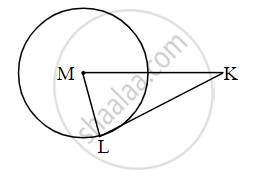
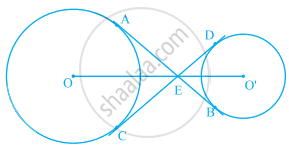
In figure, the common tangent, AB and CD to two circles with centres O and O' intersect at E. Prove that the points O, E, O' are collinear.
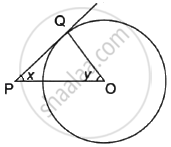
In the given figure, PQ is a tangent to the circle with centre O. If ∠OPQ = x, ∠POQ = y, then x + y is ______.
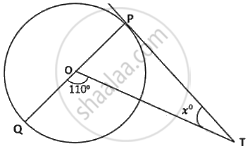
In the adjoining diagram, O is the centre of the circle and PT is a tangent. The value of x is ______.