Advertisements
Advertisements
प्रश्न
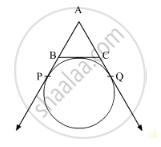
In Figure 1, AP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC
= 4 cm, then the length of AP (in cm) is
पर्याय
A. 7.5
B. 15
C. 10
D. 9
उत्तर
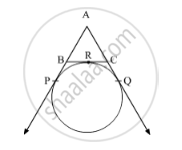
AP, AQ and BC are tangents to the circle. Suppose BC touch the circle at R.
It is given that AB = 5 cm, AC = 6 cm and BC = 4 cm.
We know that, the lengths of tangents drawn from an external point to a circle are equal.
∴ AP = AQ … (1)
PB = BR … (2)
CQ = CR .... (3)
2AP = AP + AP
∴ 2AP = AP + AQ [Using (1)]
⇒ 2AP = (AB + PB) + (AC + CQ)
⇒ 2AP = (AB + BR) + (AC + CR) [Using (2) and (3)]
⇒ 2AP = AB + (BR + CR) + AC
⇒ 2AP = AB + BC + AC
⇒ 2AP = 5 cm + 4 cm + 6 cm
⇒ 2AP = 15 cm
⇒ AP = 7.5 cm
Thus, the length of AP is 7.5 cm.
Hence, the correct answer is A.
APPEARS IN
संबंधित प्रश्न
The common point of a tangent to a circle and the circle is called ______.
In Fig. 1, AOB is a diameter of a circle with centre O and AC is a tangent to the circle at A. If ∠BOC = 130°, the find ∠ACO.

In Figure 3, a right triangle ABC, circumscribes a circle of radius r. If AB and BC are of lengths of 8 cm and 6 cm respectively, find the value of r.

In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (ii) radius of the circle.

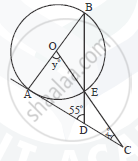
In the given figure AC is a tangent to the circle with centre O.
If ∠ADB = 55° , find x and y. Give reasons for your answers.
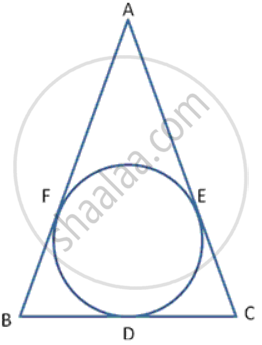
In following figure , the incircle of Δ ABC , touches the sides BC , CA and AB at D , E and F respectively. Show AF + BD + CE = AE + BF + CD
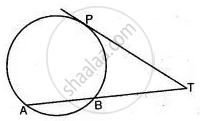
In the figure given below, PT is a tangent to the circle. Find PT if AT = 16 cm and AB = 12 cm.
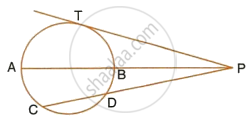
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find:
- AB.
- the length of tangent PT.
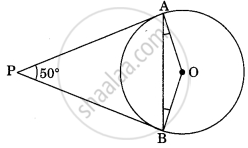
In the figure, if PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠OAB is equal to ______.
Assertion (A): A tangent to a circle is perpendicular to the radius through the point of contact.
Reason (R): The lengths of tangents drawn from an external point to a circle are equal.
