Advertisements
Advertisements
प्रश्न
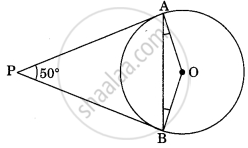
In the figure, if PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠OAB is equal to ______.
पर्याय
25°
30°
40°
50°
उत्तर
In the figure, if PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠OAB is equal to 25°.
Explanation:
Given: A circle with center O and PA and PB are tangents to circle from a common external point P to point A and B respectively and ∠APB = 50°
To find: ∠OAB
OA ⊥ AP and OB ⊥ PB ...[As tangent to at any point on the circle is perpendicular to the radius through point of contact]
∠OBP = ∠OAP = 90° ...[1]
In Quadrilateral AOBP ...[By angle sum property of quadrilateral]
∠OBP + ∠OAP + ∠AOB + ∠APB = 360°
90° + 90° + ∠AOB + 50° = 360°
∠AOB = 130° ...[2]
Now in ΔOAB
OA = OB ...[Radii of same circle]
∠OBA = ∠OAB ...[3]
Also, By angle sum property of triangle
∠OBA + ∠OAB + ∠AOB = 180°
∠OAB + ∠OAB + 130° = 180° ...[Using 2 and 3]
2∠OAB = 50°
∠OAB = 25°
संबंधित प्रश्न
In the figure given below, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT = 60°, find ∠PRQ.

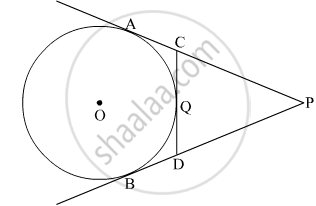
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

In the following figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
In fig. 5 is a chord AB of a circle, with centre O and radius 10 cm, that subtends a right angle at the centre of the circle. Find the area of the minor segment AQBP. Hence find the area of major segment ALBQA. (use π = 3.14)

In Figure 5, a triangle PQR is drawn to circumscribe a circle of radius 6 cm such that the segments QT and TR into which QR is divided by the point of contact T, are of lengths 12 cm and 9 cm respectively. If the area of ΔPQR = 189 cm2, then find the lengths of sides PQ and PR.
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
In following fig., PT is tangent to the circle at T and CD is a diameter of the same circle. If PC= 3cm and PT= 6cm, find the radius of the circle.
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO = 30°,
find: (i) ∠ BCO (ii) ∠ AOB (iii) ∠ APB
Tangents from an external point to a circle are ______
