Advertisements
Advertisements
प्रश्न
In fig. 5 is a chord AB of a circle, with centre O and radius 10 cm, that subtends a right angle at the centre of the circle. Find the area of the minor segment AQBP. Hence find the area of major segment ALBQA. (use π = 3.14)

उत्तर

Given: Radius of the circle, r = 10 cm
Area of the circle = \[\pi \left( 10 \right)^2 = 3 . 14 \times 100 = 314 {cm}^2\]
\[ = \frac{1}{4} \times 314 \left[ From \left( 1 \right) \right]\]
\[ = 78 . 5 {cm}^2\]
\[ = \frac{1}{2} \times 10 \times 10\]
\[ = 50 {cm}^2\]
Area of the minor segment AQBP = Area of the sector OAPB − Area of the triangle BOA
= (78.5 − 50) cm2
= 28.5 cm2
= (314 − 28.5) cm2
= 285.5 cm2
APPEARS IN
संबंधित प्रश्न
In Fig. 1, AOB is a diameter of a circle with centre O and AC is a tangent to the circle at A. If ∠BOC = 130°, the find ∠ACO.

From a point Q, 13 cm away from the centre of a circle, the length of tangent PQ to the circle is 12 cm. The radius of the circle (in cm) is
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
Find the length of the tangent from a point which is at a distance of 5cm from the centre of the circle of radius 3cm.
Construct a tangent to a circle with centre O and radius 3.5 cm at a point P on it.
In Fig. the incircle of ΔABC touches the sides BC, CA, and AB at D, E respectively. Show that: AF + BD + CE = AE + BF + CD = `1/2`( Perimeter of ΔABC)

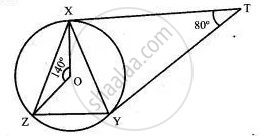
In the alongside, figure, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°. Calculate the value of ∠ZXY.
Two parallel lines touch the circle at
points A and B respectively. If the area of the circle is 25 n cm2, then AB is equal to ______

In the above figure, seg AB and seg AD are tangent segments drawn to a circle with centre C from exterior point A, then prove that: ∠A = `1/2` [m(arc BYD) - m(arc BXD)]
