Advertisements
Advertisements
प्रश्न

In the above figure, seg AB and seg AD are tangent segments drawn to a circle with centre C from exterior point A, then prove that: ∠A = `1/2` [m(arc BYD) - m(arc BXD)]
उत्तर
Proof: From figure

Seg AB ⊥ seg BC and seg AD ⊥ seg CD .......[By tangent theorem]
∴ ∠ABC = ∠ADC = 90°
In □ABCD,
∠A + ∠B + ∠C + ∠D = 360° ......[Angle of the square]
∴ ∠A + 90° + ∠C + 90° = 360°
∴ ∠A + ∠C = 360° – 180°
∴ ∠A + ∠C = 180°
∴ ∠A + m(arc BXD) = 180° [Central angle] ......(i)
Now, m(arc BXD) + m(arc BYD) = 360° ......[Two arcs contribute a complete circle] ......(ii)
Now, multiply equation (i) by 2 on both sides
2[∠A + m(arc BXD)] = 2 × 180°
∴ 2∠A + 2 × m(arc BXD) = 360°
∴ 2∠A = 360 – 2 × m(arc BXD)
∴ 2∠A = m(arc BXD) + m(arc BYD) – 2m(arc BXD)
∴ 2∠A = m(arc BYD) – m(arc BXD) .....[From (ii)]
∴ ∠A = `1/2` [m(arc BYD) – m(arc BXD)]
Hence proved.
APPEARS IN
संबंधित प्रश्न
A line intersecting a circle in two points is called a ______.
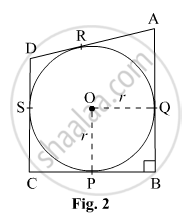
In Fig.2, a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively, If AB = 29 cm, AD = 23 cm, ∠B = 90° and DS = 5 cm, then the radius of the circle (in cm.) is:
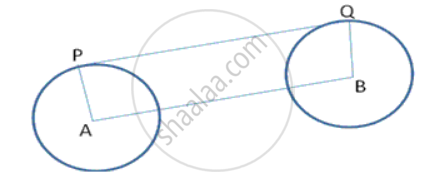
A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisects the arc PRQ.
Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
The length of the direct common tangent to two circles of radii 12cm and 4cm is 15cm. calculate the distance between their centres.
Calculate the length of direct common tangent to two circles of radii 3cm and Bern with their centres 13cm apart.
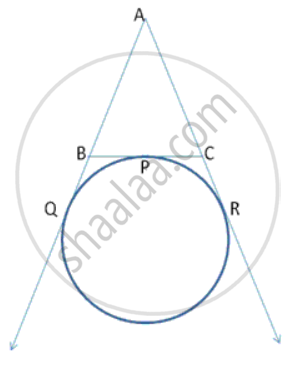
In following fig., a circle is touching the side BC of Δ ABC at P and AB and AC produced at Q and R respectively. Prove that AQ is half the perimeter of Δ ABC.
If Δ PQR is isosceles with PQ = PR and a circle with centre O and radius r is the incircle of the Δ PQR touching QR at T, prove that the point T bisects QR.
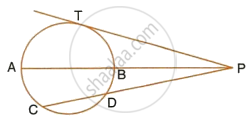
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate ∠ PAD.

ABC is a right triangle with angle B = 90º. A circle with BC as diameter meets by hypotenuse AC at point D. Prove that: BD2 = AD × DC.
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find:
- AB.
- the length of tangent PT.
In figure, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°. Then AT is equal to ______.

The tangents drawn at the extremities of the diameter of a circle are ______.
In the figure, PQ and PR are tangents to a circle with centre A. If ∠QPA=27°, then ∠QAR equals to ______
Construct a pair of tangents to a circle of radius 4 cm, which are inclined to each other at an angle of 60°.
In the given figure, AB is diameter of a circle centered at O. BC is tangent to the circle at B. If OP bisects the chord AD and ∠AOP = 60°, then find ∠C.
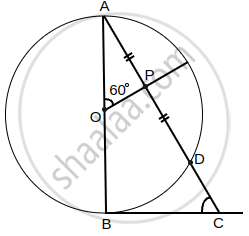
The length of tangent drawn to a circle of radius 9 cm from a point 41 cm from the centre is ______.
How many tangents can be drawn to a circle from a point on it?
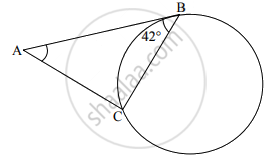
In the given figure, AB and AC are tangents to the circle. If ∠ABC = 42°, then the measure of ∠BAC is ______.
