Advertisements
Advertisements
प्रश्न
□ABCD is a parallelogram. Point P is the midpoint of side CD. seg BP intersects diagonal AC at point X, then prove that: 3AX = 2AC
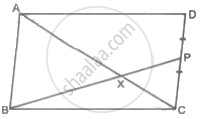
उत्तर
Proof: From the figure, in ΔABX and ΔCPX
As, AB || CD
∠BAX = ∠PCX ......[Alternate angle]
∠BXA = ∠PXC ........[Vertically opposite angles]
∴ ΔABX ∼ ΔCPX .......[By AA similarity theorem]
We know that,
Similar triangles have comparable side ratios that are similar to or equal.
∴ `("AX")/("CX") = ("AB")/("CP")`
But CD = AB and 'P' is mid-point of CD.
∴ AB = 2CP
∴ `("AX")/(("AC" - "AX")) = (2"CP")/("CP")`
∴ `("AX")/(("AC" - "AX"))` = 2
∴ AX = 2(AC – AX)
∴ AX = 2AC – 2AX
∴ AX + 2AX = 2AC
∴ 3AX = 2AC
Hence proved.
APPEARS IN
संबंधित प्रश्न
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:

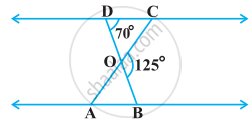
In the following figure, ΔODC ∼ ΔOBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.
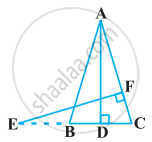
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔABD ∼ ΔCBE
In the following figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that ΔABD ∼ ΔECF.
A vertical stick 10 cm long casts a shadow 8 cm long. At the same time a shadow 30 m long. Determine the height of the tower.
In the following figure, AB || QR. Find the length of PB.

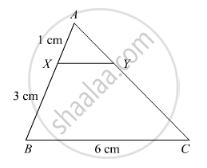
In the following figure, XY || BC. Find the length of XY.
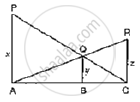
In the following figure, PA, QB and RC are each perpendicular to AC. Prove that `1/x+1/z=1/y`
The sides of certain triangles are given below. Determine which of them right triangles are.
9cm, 16cm, 18cm
In the given figure MN|| BC and AM: MB= 1: 2
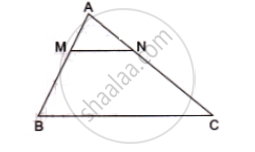
find ` (area(ΔAMN))/(area(ΔABC))`
It is given that ΔDEF ~ ΔRPQ. Is it true to say that ∠D = ∠R and ∠F = ∠P? Why?
In a ∆PQR, PR2 – PQ2 = QR2 and M is a point on side PR such that QM ⊥ PR. Prove that QM2 = PM × MR.
If ∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12 cm, find the perimeter of ∆ABC.
Areas of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.
In figure, if ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm and CP = 4 cm, then find the lengths of PD and CD.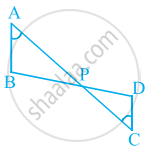
A street light bulb is fixed on a pole 6 m above the level of the street. If a woman of height 1.5 m casts a shadow of 3 m, find how far she is away from the base of the pole.
In figure, ABC is a triangle right angled at B and BD ⊥ AC. If AD = 4 cm, and CD = 5 cm, find BD and AB.
Which of the following conditions is not sufficient to determine the congruence of two triangles?
Diagonals of a trapezium PQRS intersect each other at the point O, PQ || RS and PQ = 3 RS. Find the ratio of the areas of triangles POQ and ROS.
