Advertisements
Advertisements
प्रश्न
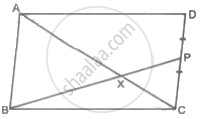
In the following figure, PA, QB and RC are each perpendicular to AC. Prove that `1/x+1/z=1/y`
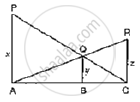
In the given figure, PA, QB and RC are perpendicular to AC. If PA = x units, QB = units and RC = z units, prove that `1/x+1/z=1/y`.
उत्तर
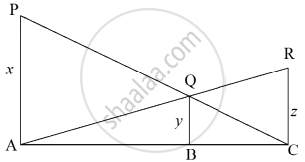
We have, PA ⊥ AC, QB ⊥ AC and RC ⊥ AC
Let, AB = a and BC = b
In ΔCQB and ΔCPA
∠QCB = ∠PCA ...[Common]
∠QBC = ∠PAC ...[Each 90°]
Then, ΔCQB ~ ΔCPA ...[By AA similarity]
`therefore"QB"/"PA"="CB"/"CA"` ...[Corresponding parts of similar Δ are proportional]
`rArry/x=b/(a+b)` ...(i)
In ΔAQB and ΔARC
∠QAB = ∠RAC ...[Common]
∠ABQ = ∠ACR ...[Each 90°]
Then, ΔAQB ~ ΔARC ...[By AA similarity]
`therefore"QB"/"RC"="AB"/"AC"` ...[Corresponding parts of similar Δ are proportional]
`rArry/z=a/(a+b)` ...(ii)
Adding equations (i) & (ii)
`y/x+y/z=b/(a+b)+a/(a+b)`
`rArry(1/x+1/z)=(b+a)/(a+b)`
`rArry(1/x+1/z)=1`
`rArr1/x+1/z=1/y`
संबंधित प्रश्न
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:

D is the mid-point of side BC of a ΔABC. AD is bisected at the point E and BE produced cuts AC at the point X. Prove that BE : EX = 3 : 1
ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the AB and BC.
Two triangles ABC and PQR are such that AB = 3 cm, AC = 6cm, ∠𝐴 = 70°, PR = 9cm ∠𝑃 = 70° and PQ = 4.5 cm. Show that ΔABC ∼ΔPQR and state that similarity criterion.
Two triangles DEF an GHK are such that ∠D = 48° and ∠H = 57° . If ΔDEF ∼GHK then find the measures of ∠F
In a ∆PQR, PR2 – PQ2 = QR2 and M is a point on side PR such that QM ⊥ PR. Prove that QM2 = PM × MR.
In figure, if DE || BC, find the ratio of ar(ADE) and ar(DECB).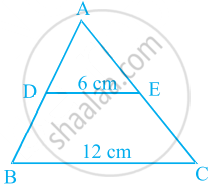
In figure, if ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm and CP = 4 cm, then find the lengths of PD and CD.
It is given that ΔABC ~ ΔDFE, ∠A =30°, ∠C = 50°, AB = 5 cm, AC = 8 cm and DF = 7.5 cm. Then, the following is true ______.
□ABCD is a parallelogram. Point P is the midpoint of side CD. seg BP intersects diagonal AC at point X, then prove that: 3AX = 2AC