Advertisements
Advertisements
Questions
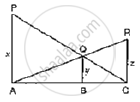
In the following figure, PA, QB and RC are each perpendicular to AC. Prove that `1/x+1/z=1/y`
In the given figure, PA, QB and RC are perpendicular to AC. If PA = x units, QB = units and RC = z units, prove that `1/x+1/z=1/y`.
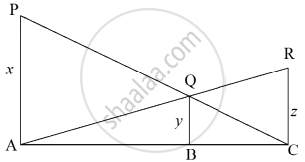
Solution
We have, PA ⊥ AC, QB ⊥ AC and RC ⊥ AC
Let, AB = a and BC = b
In ΔCQB and ΔCPA
∠QCB = ∠PCA ...[Common]
∠QBC = ∠PAC ...[Each 90°]
Then, ΔCQB ~ ΔCPA ...[By AA similarity]
`therefore"QB"/"PA"="CB"/"CA"` ...[Corresponding parts of similar Δ are proportional]
`rArry/x=b/(a+b)` ...(i)
In ΔAQB and ΔARC
∠QAB = ∠RAC ...[Common]
∠ABQ = ∠ACR ...[Each 90°]
Then, ΔAQB ~ ΔARC ...[By AA similarity]
`therefore"QB"/"RC"="AB"/"AC"` ...[Corresponding parts of similar Δ are proportional]
`rArry/z=a/(a+b)` ...(ii)
Adding equations (i) & (ii)
`y/x+y/z=b/(a+b)+a/(a+b)`
`rArry(1/x+1/z)=(b+a)/(a+b)`
`rArry(1/x+1/z)=1`
`rArr1/x+1/z=1/y`
RELATED QUESTIONS
S and T are point on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ∼ ΔRTS.
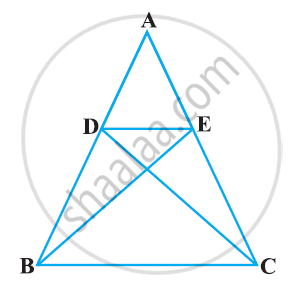
In the following figure, if ΔABE ≅ ΔACD, show that ΔADE ∼ ΔABC.
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔABD ∼ ΔCBE
In the following figure, AB || QR. Find the length of PB.

In ΔABC~ΔDEF such that 2AB = DE and BC = 6cm, find EF.
In a trapezium ABCD, it is given that AB║CD and AB = 2CD. Its diagonals AC and BD intersect at the point O such that ar(ΔAOB) = 84cm2. Find ar(ΔCOD).
In the figure, if DE∥BC, AD = 3cm, BD = 4cm and BC= 14 cm, then DE equals ______.
D is a point on side QR of ΔPQR such that PD ⊥ QR. Will it be correct to say that ΔPQD ~ ΔRPD? Why?
ABCD is a trapezium with AD ∥ BC and AD = 4 cm. If the diagonals AC and BD intersect each other at O such that AO/OC = DO/OB = 1/2, then BC = ______.
In the given figure, CM and RN are respectively the medians of ΔABC and ΔPQR. If ΔABC ∼ ΔPQR, then prove that ΔAMC ∼ ΔPNR.