English Medium
Academic Year: 2024-2025
Date & Time: 10th March 2025, 10:30 am
Duration: 3h
Advertisements
General Instructions:
Read the following instructions very carefully and strictly follow them:
- This question paper contains 38 questions. All questions are compulsory.
- This question paper is divided into five Sections - A, B, C, D and E.
- In Section A, Questions no. 1 to 18 are multiple choice questions (MCQs) and questions number 19 and 20 are Assertion-Reason based questions of 1 mark each.
- In Section B, Questions no. 21 to 25 are very short answer (VSA) Lype questions, carrying 2 marks each.
- In Section C, Questions no. 26 to 31 are short answer (SA) type questions, carrying 3 marks cach.
- In Section D, Questions no. 32 to 35 are long answer (LA) type questions carrying 5 marks each.
- In Section E, Questions no. 36 to 38 are case study based questions carrying 4 marks each. Internal choice is provided in 2 marks questions in each case study.
- There is no overall choice. However, an internal choice has been provided in 2 questions in Section B, 2 questions in Section C, 2 questions in Section D and 3 questions in Section E.
- Draw neat diagrams wherever required. Take `pi = 22/7` wherever required,
if not stated. - Use of calculator is not allowed.
If tan 30 = `sqrt 3` then `theta/2` equals ______.
60°
30°
20°
10°
Chapter:
If x is the LCM of 4, 6, 8 and y is the LCM of 3, 5, 7 and p is the LCM of x and y, then which of the following is true?
p = 35x
p = 4y
p = 8x
p = 16y
Chapter:
The value of 'k' for which the system of linear equations 6x + y = 3k and 36x + 6y = 3 have infinitely many solutions is ______.
6
`1/6`
`1/2`
`1/3`
Chapter:
If α and β are the zeroes of the polynomial p(x) = x2 − ax − b, then the value of (α + β + αβ) is equal to ______.
a + b
− a − b
a − b
− a + b
Chapter:
If `x/12 - 3/x` = 0, then the values of x are ______.
± 6
± 4
± 12
± 13
Chapter:
The line represented by `x/4 + y/6 = 1`, intersects the x-axis and y-axis, respectively, at P and Q. The coordinates of the mid-point of line segment PQ are ______.
(2, 3)
(3, 2)
(2, 0)
(0, 3)
Chapter:
Two of the vertices of ΔPQR are P(−1, 5) and Q(5, 2). The coordinates of a point which divides PQ in the ratio 2 : 1 are ______.
(3, −3)
(5, 5)
(3, 3)
(5, 1)
Chapter:
If tangents PA and PB from a point P to a circle with centre O are inclined to each other an angle of 80°, then ∠POA is equal to ______.
50°
60°
70°
80°
40°
Chapter: [0.042] Circles
(cot θ + tan θ) equals ______.
cosec θ sec θ
sin θ sec θ
cos θ tan θ
sin θ cos θ
Chapter:
If in ∆DEF and ∆PQR, ∠D ≅ ∠Q, ∠R ≅ ∠E then which of the following statements is false?

`("EF")/("PR") = ("DF")/("PQ")`
`("DE")/("PQ") = ("EF")/("RP")`
`("DE")/("QR") = ("DF")/("PQ")`
`("EF")/("RP") = ("DE")/("QR")`
`("EF")/("PR") = ("DF")/("PQ")`
Chapter: [0.040999999999999995] Triangles [0.040999999999999995] Triangles [0.040999999999999995] Triangles
The measurements of ΔLMN and ΔABC are shown in the figure given below. The length of side AC is ______.
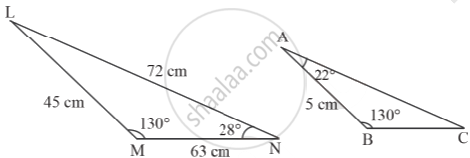
16 cm
7 cm
8 cm
4 cm
Chapter:
If the volumes of two cubes are in the ratio 8:125, then the ratio of their surface areas is ______.
8:125
4:25
2:5
16:25
Chapter:
If the area of a sector of a circle of radius 36 cm is 54π cm2, then the length of the corresponding arc of the sector is ______.
8π cm
6π cm
4π cm
3π cm
Chapter:
A die is thrown once. The probability of getting a number which is not a factor of 36, is ______.
`1/2`
`2/3`
`1/6`
`5/6`
Chapter:
If the mean of 2, 9, x + 6, 2x + 3, 5, 10, 5 is 7, then the value of x is ______.
9
6
5
3
Chapter:
AOBC is a rectangle whose three vertices are A(0, 2), O(0, 0) and B(4, 0). The square of the length of its diagonal is equal to ______.
36
20
16
4
Chapter:
Advertisements
Zeroes of the polynomial p(x) = `x^2 - 3sqrt2 x + 4` are ______.
`2, sqrt2`
`2sqrt2, sqrt2`
`4sqrt2, -sqrt2`
`sqrt2, 2`
Chapter:
In the given figure, in Δ ABC, AD ⊥ BC and ∠BAC = 90°. If BC = 16 cm and DC = 4 cm, then the value of x is ______.
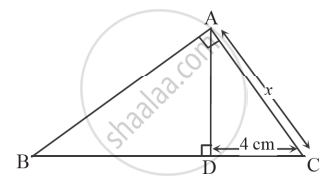
4 cm
5 cm
8 cm
3 cm
Chapter:
Assertion (A): A ladder leaning against a wall, stands at a horizontal distance of 6 m from the wall. If the height of the wall up to which the ladder reaches is 8 m, then the length of the ladder is 10 m.
Reason (R): The ladder makes an angle of 60° with the ground.
Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of the Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of the Assertion (A).
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Chapter:
Assertion (A): If two tangents are drawn to a circle from an external point, then they subtend equal angles at the centre of the circle.
Reason (R): A parallelogram circumscribing a circle is a rhombus.
Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of the Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of the Assertion (A).
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Chapter:
If 4k = tan2 60° − 2 cosec2 30° − 2 tan2 30°, then find the value of k.
Chapter:
The probability of guessing the correct answer of a certain test question is `x/12`. If the probability of not guessing the correct answer is `5/6` then find the value of x.
Chapter:
Find the smallest number which is divisible by both 644 and 462.
Chapter:
Two numbers are in the ratio 4:5 and their HCF is 11. Find the LCM of these numbers.
Chapter:
Find the value(s) of 'k' so that the quadratic equation 4x2 + kx + 1 = 0 has real and equal roots.
Chapter:
If ‘α’ and ‘β’ are the zeroes of the polynomial p(y) = y2 − 5y + 3, then find the value of α4β3 + α3β4.
Chapter:
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Chapter: [0.042] Circles
If the mid-point of the line segment joining the points A(3, 4) and B(k, 6) is P(x, y) and x + y − 10 = 0, find the value of k.
Chapter:
Find the coordinates of the points which divide the line segment joining A (−2, 2) and B (2, 8) into four equal parts.
Chapter: [0.031] Lines (In Two-dimensions)
Advertisements
Prove that `(5 sqrt3 + 2/3)` is an irrational number given that `sqrt3` is an irrational number.
Chapter:
Prove that:
`sqrt((sec A - 1)/(sec A + 1)) + sqrt((sec A + 1)/(sec A - 1))` = 2 cosec A.
Chapter:
Prove that:
`(1/(cos A) - cos A)(1/(sin A) - sin A) = 1/(tan A + cot A)`
Chapter:
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the minor segment. [Use π = 3.14.]
Chapter: [0.061] Areas Related to Circles
Three unbiased coins are tossed simultaneously. Find the probability of getting:
- exactly two tails
- at least one head
- at most two heads
Chapter:
In the given figure, PC is a tangent to the circle at C. AOB is the diameter which when extended meets the tangent at P. Find ∠CBA and ∠BCO, if ∠PCA = 110°.
Chapter:
The perimeter of an isosceles triangle is 32 cm. If each equal side is `5/6` th of the base, find the area of the triangle.
Chapter:
The sum of the third and the seventh terms of an AP is 6 and their product is 8. Find the sum of first sixteen terms of the AP.
Chapter: [0.024] Arithmetic Progressions
The minimum age of children eligible to participate in a painting competition is 8 years. It is observed that the age of the youngest boy was 8 years, and the ages of the participants, when seated in order of age, have a common difference of 4 months. If the sum of the ages of all the participants is 168 years, find the age of the eldest participant in the painting competition.
Chapter:
In the following figure, PA, QB and RC are each perpendicular to AC. Prove that `1/x+1/z=1/y`
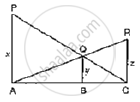
Chapter: [0.040999999999999995] Triangles
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR show that ΔABC ~ ΔPQR.
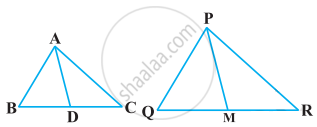
Chapter: [0.040999999999999995] Triangles
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm, are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
Chapter:
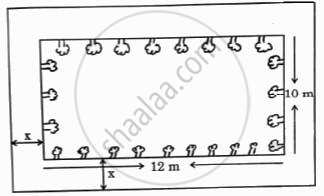
|
A garden designer is planning a rectangular lawn that is to be surrounded by a uniform walkway.
The total area of the lawn and the walkway is 360 square meters. The width of the walkway is same on all sides. The dimensions of the lawn itself are 12 meters by 10 meters. |
Based on the information given above, answer the following questions:
- Formulate the quadratic equation representing the total area of the lawn and the walkway, taking the width of the walkway = x m. (1)
-
- Solve the quadratic equation to find the width of the walkway “x”. (2)
OR - Solve the quadratic equation to find the width of the walkway “x”. (2)
- Solve the quadratic equation to find the width of the walkway “x”. (2)
- Find the perimeter of the lawn. (1)
Chapter:
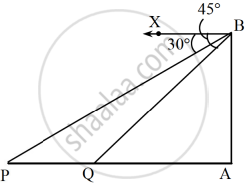
|
A lighthouse stands tall on a cliff by the sea, watching over ships that pass by. One day a ship is seen approaching the shore and from the top of the lighthouse, the angles of depression of the ship are observed to be 30° and 45° as it moves from point P to point Q. The height of the lighthouse is 50 metres.
|
Based on the information given above, answer the following questions:
- Find the distance of the ship from the base of the lighthouse when it is at point Q, where the angle of depression is 45°. (1)
- Find the measures of ∠PBA and ∠QBA. (1)
-
- Find the distance travelled by the ship between points P and Q. (2)
OR - If the ship continues moving towards the shore and takes 10 minutes to travel from Q to A, calculate the speed of ship in km/h, from Q to A. (2)
- Find the distance travelled by the ship between points P and Q. (2)
Chapter:
| The India Meteorological Department observer seasonal and annual rainfall every year in different sub-divisions of our country. It helps them to compare and analyze the results.
The table below shows sub-divisions wise seasonal (monsoon) rainfall (in mm) in 2023:
|
Based on the information given above, answer the following questions:
- Write the modal class. (1)
-
- Find the median of the given data. (2)
OR - Find the mean rainfall in the season. (2)
- Find the median of the given data. (2)
- If a sub-division having at least 800 mm rainfall during monsoon season is considered a good rainfall sub-division, then how many sub-divisions had good rainfall? (1)
Chapter:
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
CBSE previous year question papers Class 10 Mathematics with solutions 2024 - 2025
Previous year Question paper for CBSE Class 10 Maths-2025 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of CBSE Class 10.
How CBSE Class 10 Question Paper solutions Help Students ?
• Question paper solutions for Mathematics will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.