Question

In the given figure, PC is a tangent to the circle at C. AOB is the diameter which when extended meets the tangent at P. Find ∠CBA and ∠BCO, if ∠PCA = 110°.

Answer 1

Here, AB is a diameter of the circle from point C, and a tangent is drawn which meets at a point P.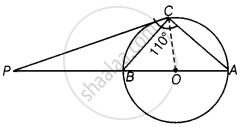

Join OC.

Here, OC is radius.

Since, tangent at any point of a circle is perpendicular to the radius through point of contact circle.

∴ OC ⊥ PC

Now, ∠PCA = 110°   ...[Given]

⇒ ∠PCO + ∠OCA = 110°

⇒ 90° + ∠OCA = 110°

⇒ ∠OCA = 20°

∴ OC = OA = Radius of circle

⇒ ∠OCA = ∠OAC = 20°   ...[Since, two sides are equal, then their opposite angles are equal]

Since, PC is a tangent,

So ∠BCP = ∠CAB = 20°      ...[Angles in a alternate segment are equal]

In ΔPBC,

∠P + ∠C + ∠A = 180°

∠P = 180° – (∠C + ∠A)

= 180° – (110° + 20°)

= 180° – 130°

= 50°

In ΔPBC,

∠BPC + ∠PCB + ∠PBC = 180°     ...[Sum of all interior angles of any triangle is 180°]

⇒ 50° + 20° + ∠PBC = 180°

⇒ ∠PBC = 180° – 70°

⇒ ∠PBC = 110°

Since APB is a straight line.

∴ ∠PBC + ∠CBA = 180°

⇒ ∠CBA = 180° – 110°

⇒ ∠CBA = 70°