Question

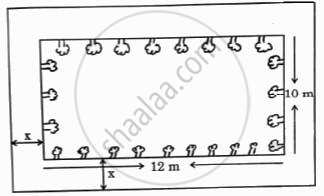
A garden designer is planning a rectangular lawn that is to be surrounded by a uniform walkway. The total area of the lawn and the walkway is 360 square meters. The width of the walkway is same on all sides. The dimensions of the lawn itself are 12 meters by 10 meters.

Based on the information given above, answer the following questions:

1. Formulate the quadratic equation representing the total area of the lawn and the walkway, taking the width of the walkway = x m.   (1)
2. 1. Solve the quadratic equation to find the width of the walkway “x”.   (2)
                                    OR
      
   2. Solve the quadratic equation to find the width of the walkway “x”.   (2)
3. Find the perimeter of the lawn.   (1)

Answer 1

Given:

The dimensions of the lawn:

Length = 12 m, Breadth = 10 m

The total area (lawn + walkway) = 360 m²

The breadth of the walkway = x meters (same on all sides)

i. Formulate the quadratic equation

The total dimensions including the walkway:

Total length = 12 + 2x (walkway added on both sides)

Total breadth = 10 + 2x (walkway added on both sides)

Total area equation:

(12 + 2x)(10 + 2x) = 360

⇒ 120 + 24x + 20x + 4x² = 360

⇒ 4x² + 44x + 120 = 360

⇒ 4x² + 44x + 120 − 360 = 0

⇒ 4x² + 44x − 240  = 0

⇒ x² + 11x − 60  = 0           ...(Dividing the entire equation by 4)

This is the required quadratic equation.

ii. (a) Solve the quadratic equation for x

x² + 11x − 60  = 0

⇒ x² + 15x − 4x − 60  = 0           ...[Factorizing ∴ (+11 = +15 - 4)]

⇒ x(x + 15) − 4(x + 15) = 0

⇒ (x + 15)(x − 4) = 0

⇒ x + 15 = 0 or x − 4 = 0

⇒ x = −15 or x = 4

Since breadth cannot be negative, we take:

∴ x = 4

So, the breadth of the walkway is 4 metres.

ii. (b) The area of the walkway:

The rate of paving is ₹ 50 m².

∴ Area × rate = 12000

Area = `12000/50`

= 240 m²

iii. The Perimeter of the Lawn

The perimeter of the rectangular lawn is given by

⇒ P = 2(Length + Breadth)

⇒ P = 2(12 + 10)

⇒ P = 2 × 22

⇒ P = 44 m