Question

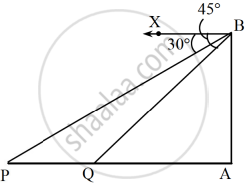
A lighthouse stands tall on a cliff by the sea, watching over ships that pass by. One day a ship is seen approaching the shore and from the top of the lighthouse, the angles of depression of the ship are observed to be 30° and 45° as it moves from point P to point Q. The height of the lighthouse is 50 metres.

Based on the information given above, answer the following questions:

1. Find the distance of the ship from the base of the lighthouse when it is at point Q, where the angle of depression is 45°.   (1)
2. Find the measures of ∠PBA and ∠QBA.   (1)
3. 1.  Find the distance travelled by the ship between points P and Q.   (2)
                                     OR
   2. If the ship continues moving towards the shore and takes 10 minutes to travel from Q to A, calculate the speed of ship in km/h, from Q to A.   (2)

Answer 1

(i) ΔABQ,

tan 45° = `"AB"/"AQ"`

tan 45° = `50/x`

1 = `50/x`

x = 50 m

∴ AQ = 50 m

(ii) ∠PBA = 90 − 30

∴ ∠PBA = 60

∠QBA = 90 − 45

∴ ∠QBA = 45

(iii) a. ΔAPB,

tan 30 = `"AB"/"AP"`

`1/sqrt3= 50/"AP"`

∴ AP = `50sqrt3`

PQ = AP - AQ 

= `50sqrt3` − 50

= `50 (sqrt3-1)`

OR

b. t_QA = 10mm = `10/60`

= `1/6` h

Speed = `d/t`

= `"QA"/"t"`

= `(50/1000)/(1/6)`

= `5/100xx6/1`

= `30/100`

= 0.3 km/h