Advertisements
Advertisements
Questions
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the minor segment. [Use π = 3.14.]
A chord of a circle of radius 10 cm subtends a right angle at the centre of the circle. Find the area of the corresponding minor segment. [Use π = 3.14]
Solution 1

Let AB be the chord of a circle subtending an angle of 90° at the centre O of the circle.
Area of sector = `theta/(360^circ) x pi^2`
`= (90^circ)/(360^circ) xx 314 /100 xx 10xx10` cm2
= `1/4 xx 314` cm2
`= 157/2` cm2
= 78.5 cm2
Corresponding minor segment = ΔAOB
= 78.5 cm2 − `[1/2 xx10 xx10]`
= 78.5 cm2 − 50 cm2
= 28.5 cm2
Solution 2

Area of minor segment = Area of sector AOBC − Area of right triangle AOB
`=theta/360^circpi("OA")^2 - 1/2xx` OA× OB `
`= 90^circ/360^circxx3.14(10)^2 - 1/2xx10xx10`
= 78.5 − 50
= 28.5 cm2
Hence, the area of minor segment is 28.5 cm2
Notes
Students should refer to the answer according to their question and preferred marks.
APPEARS IN
RELATED QUESTIONS
Find the area of the sector whose arc length and radius are 14 cm and 6 cm respectively.
A car has two wipers which do not overlap. Each wiper has blade of length 25 cm sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades [Use π = `22/7`]
A sector of circle of radius 4cm contains an angle of 30°. Find the area of sector
The area of sector of circle of radius 5cm is 5𝜋 cm2. Find the angle contained by the sector.
A sector of 56° cut out from a circle contains area of 4.4 cm2. Find the radius of the circle
A chord of a circle subtends an angle 𝜃 at the centre of circle. The area of the minor segment cut off by the chord is one eighth of the area of circle. Prove that 8 sin`theta/2 "cos"theta/2+pi =(pitheta)/45`
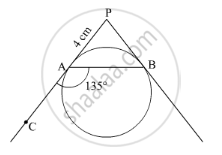
In the given figure, PA and PB are tangents to a circle from an external point P such that PA = 4 cm and ∠BAC = 135°. Find the length of chord AB ?

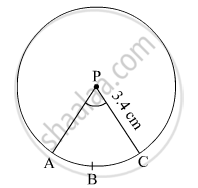
In the given figure, radius of circle is 3.4 cm and perimeter of sector P-ABC is 12.8 cm . Find A(P-ABC).
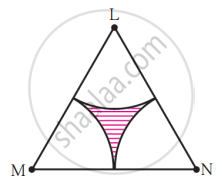
(2) Area of any one of the sectors
In the given figure, if A is the centre of the circle. \[\angle\] PAR = 30°, AP = 7.5, find the area of the segment PQR. (\[\pi\] = 3.14)

In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

Choose the correct alternative answer for the following question.
Find the perimeter of a sector of a circle if its measure is 90° and radius is 7 cm.
In a circle of radius 7 cm, a square ABCD is inscribed. Find the area of the circle which is outside the square.
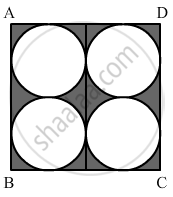
In the given figure, find the area of the shaded region, where ABCD is a square of side 14 cm and all circles are of the same diameter.
A chord 10 cm long is drawn in a circle whose radius is `5sqrt(2)` cm. Find the areas of both the segments.
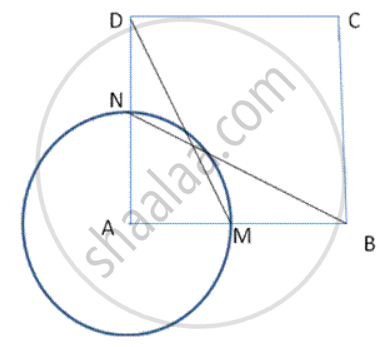
In following fig., ABCD is a square. A cirde is drawn with centre A so that it cuts AB and AD at Mand N respectively. Prove that Δ DAM ≅ Δ .BAN.
Find the area of the sector whose arc length and radius are 8 cm and 3 cm respectively.
Find the area of the sector of a circle of radius 8 cm and arc with length 15 cm.
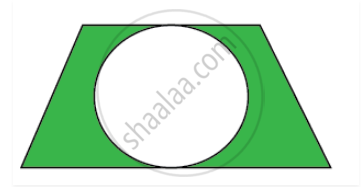
In the given figure, a circle is inscribed in a trapezium of height 14 cm and lengths of parallel sides are equal to 25 cm and 40 cm. What is the area of the shaded region?