Advertisements
Advertisements
Question
In the given figure, radius of circle is 3.4 cm and perimeter of sector P-ABC is 12.8 cm . Find A(P-ABC).
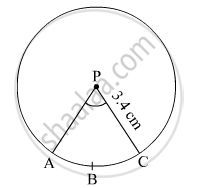
Solution
Radius of the circle, r = 3.4 cm
Perimeter of sector P-ABC = 12.8 cm
Let l be the length of the arc ABC.
∴ l + 2r = 12.8 cm
⇒ l + 2 × 3.4 = 12.8
⇒ l = 12.8 − 6.8 = 6 cm
∴ A(P-ABC) = Area of the sector PABC = \[\frac{1}{2}lr = \frac{1}{2} \times 6 \times 3 . 4\] = 10.2 cm2
Thus, A(P-ABC) is 10.2 cm2.
APPEARS IN
RELATED QUESTIONS
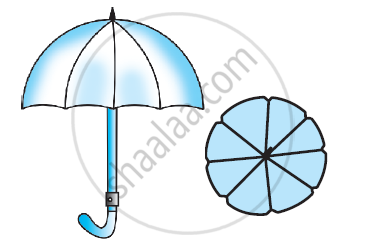
An umbrella has 8 ribs which are equally spaced. Assuming umbrella to be a flat circle of radius 45 cm. Find the area between the two consecutive ribs of the umbrella.
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding:
Major sector [Use π = 3.14]
To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships warned. [Use π = 3.14]
The area of sector of circle of radius 5cm is 5𝜋 cm2. Find the angle contained by the sector.
AB is a chord of circle with centre O and radius 4cm. AB is length of 4cm. Find the area of sector of the circle formed by chord AB
In a circle of radius 35 cm, an arc subtends an angle of 72° at the centre. Find the length of arc and area of sector
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm and divides the circle into two segments. Find the area of the minor segment.
A chord of circle of radius 14cm makes a right angle at the centre. Find the areas of minor and major segments of the circle.
In the given figure, O is the centre of the circle. m ( arc PQR) = 60° OP = 10 cm. Find the area of the shaded region.( \[\pi\]= 3.14, \[\sqrt{3}\]= 1.73)

In the given figure, if A is the centre of the circle. \[\angle\] PAR = 30°, AP = 7.5, find the area of the segment PQR. (\[\pi\] = 3.14)

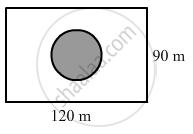
A park is in the form of a rectangle 120 m by 90 m. At the centre of the park there is a circular lawn as shown in the figure. The area of the park excluding the lawn is 2950 m2. Find the radius of the circular lawn.
The radius of a circle with centre O is 7 cm. Two radii OA and OB are drawn at right angles to each other. Find the areas of minor and major segments.
A chord 10 cm long is drawn in a circle whose radius is `5sqrt(2)` cm. Find the areas of both the segments.
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
The area of the largest square that can be inscribed in a circle of radius 12 cm is ____________.
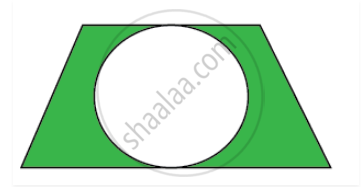
In the given figure, a circle is inscribed in a trapezium of height 14 cm and lengths of parallel sides are equal to 25 cm and 40 cm. What is the area of the shaded region?
The areas of two sectors of two different circles with equal corresponding arc lengths are equal. Is this statement true? Why?
In figure, arcs are drawn by taking vertices A, B and C of an equilateral triangle of side 10 cm. to intersect the sides BC, CA and AB at their respective mid-points D, E and F. Find the area of the shaded region (Use π = 3.14).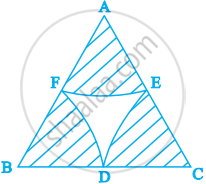
Find the area of the sector of a circle of radius 5 cm, if the corresponding arc length is 3.5 cm.
The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
