Advertisements
Advertisements
Question
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm and divides the circle into two segments. Find the area of the minor segment.
Solution
We know that the area of minor segment of angle `theta` in a circle of radius r is,
`A={(pitheta)/360^@-"sin"theta/2 "cos"theta/2}r^2`
It is given that the chord AB divides the circle in two segment.
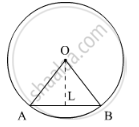
We have OA=4 cm and AB=4 cm. so,
`AL=(AB)/2 cm`
`=4/2 cm`
= 2 cm
Let `angleAOB=2theta`. Then,
`angleAOL=angleBOL`
`=theta`
In`triangleOLA`,We have
`sintheta=(AL)/(OA)`
`=2/4`
`=1/2`
`theta="sin"^(-1)1/2`
`=30^@`
Hence, `angleAOB=60^@`
Now using the value of r and `theta`, we will find the area of minor segment
`A={(pixx60^@)/360^@-"sin"60^@/2"cos"60^@/2}xx4xx4`
`={pi/6-sin30^@cos30^@}xx16`
`={(16xxpi)/6-1/2xxsqrt(3)/2xx16}`
`={(8pi)/3-4sqrt(3)}cm^2`
APPEARS IN
RELATED QUESTIONS
A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle. [Use π = 3.14 and `sqrt3 = 1.73` ]
A chord 10 cm long is drawn in a circle whose radius is 5√2 cm. Find the area of both
segments
A chord PQ of a circle with a radius of cm subtends an angle of 60° with the center of the circle. Find the area of the minor as well as the major segment. ( \[\pi\] = 3.14, \[\sqrt{3}\] = 1.73)
Choose the correct alternative answer for the following question.
Find the perimeter of a sector of a circle if its measure is 90° and radius is 7 cm.
In the given figure, ABCD is a square of side 7 cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.

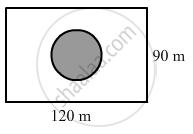
A park is in the form of a rectangle 120 m by 90 m. At the centre of the park there is a circular lawn as shown in the figure. The area of the park excluding the lawn is 2950 m2. Find the radius of the circular lawn.
Find the area of the sector whose arc length and radius are 8 cm and 3 cm respectively.
If angle of sector is 60°, radius is 3.5 cm then length of the arc is ____________.
The area of the sector of a circle with radius 6 cm and of angle 60° is ____________.
In the given figure, arcs have been drawn of radius 7 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.