Advertisements
Advertisements
प्रश्न
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm and divides the circle into two segments. Find the area of the minor segment.
उत्तर
We know that the area of minor segment of angle `theta` in a circle of radius r is,
`A={(pitheta)/360^@-"sin"theta/2 "cos"theta/2}r^2`
It is given that the chord AB divides the circle in two segment.
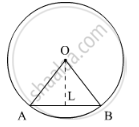
We have OA=4 cm and AB=4 cm. so,
`AL=(AB)/2 cm`
`=4/2 cm`
= 2 cm
Let `angleAOB=2theta`. Then,
`angleAOL=angleBOL`
`=theta`
In`triangleOLA`,We have
`sintheta=(AL)/(OA)`
`=2/4`
`=1/2`
`theta="sin"^(-1)1/2`
`=30^@`
Hence, `angleAOB=60^@`
Now using the value of r and `theta`, we will find the area of minor segment
`A={(pixx60^@)/360^@-"sin"60^@/2"cos"60^@/2}xx4xx4`
`={pi/6-sin30^@cos30^@}xx16`
`={(16xxpi)/6-1/2xxsqrt(3)/2xx16}`
`={(8pi)/3-4sqrt(3)}cm^2`
APPEARS IN
संबंधित प्रश्न
Find the area of the minor segment of a circle of radius 14 cm, when its central angle is 60˚. Also find the area of the corresponding major segment.[use π=22/7]
A round table cover has six equal designs, as shown in figure. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs.0.35 per cm2. [Use `sqrt3 = 1.7`]
A sector of a circle of radius 8cm contains the angle of 135°. Find the area of sector.
The radius of a circle is 17.5 cm. Find the area of the sector enclosed by two radii and an arc 44 cm in length.
A car has two wipers that do not overlap. Each wiper has a blade of length 21 cm sweeping through an angle of 120°. Find the total area cleaned at each sweep of the blades. `("Take" π =22/7)`
The areas of two sectors of two different circles with equal corresponding arc lengths are equal. Is this statement true? Why?
Find the area of the sector of a circle of radius 5 cm, if the corresponding arc length is 3.5 cm.
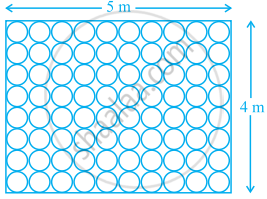
Floor of a room is of dimensions 5 m × 4 m and it is covered with circular tiles of diameters 50 cm each as shown in figure. Find the area of floor that remains uncovered with tiles. (Use π = 3.14)
What is the length of arc of a circle of radius 7 cm which subtends an angle of 90° at the centre of the circle?
Find the area of the unshaded region shown in the given figure.