Advertisements
Advertisements
प्रश्न
A round table cover has six equal designs, as shown in figure. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs.0.35 per cm2. [Use `sqrt3 = 1.7`]
उत्तर
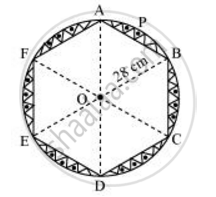
It can be observed that these designs are segments of the circle.
Consider segment APB. Chord AB is a side of the hexagon. Each chord will substitute `(360º)/6` = 60º at the centre of the circle.
In ΔOAB,
∠OAB = ∠OBA (As OA = OB)
∠AOB = 60°
∠OAB + ∠OBA + ∠AOB = 180°
2∠OAB = 180° − 60° = 120°
∠OAB = 60°
Therefore, ΔOAB is an equilateral triangle.
Area of ΔOAB = `sqrt3/4 xx ("side")^2`
`=sqrt3/4 xx (28)^2 `
` = 196sqrt3`
` = 196 xx 1.7 `
= 333.2 cm2
Area of sector OAPB = `60^@/360^@ xx pir^2`
`= 1/6xx 22/7xx28xx28`
`= 1232/3 cm^2`
Area of segment APB = Area of sector OAPB − Area of ΔOAB
`=(1232/3 - 333.2) cm^2`
Therefore, the number of designs = `6xx(1232/3 - 333.2) cm^2`
`= (2464 - 1999.2) cm^2`
= 464.8 cm2
Cost of making 1 cm2 designs = Rs 0.35
Cost of making 464.76 cm2 designs = 464.8 × 0.35 = Rs 162.68
Therefore, the cost of making such designs is Rs. 162.68.
APPEARS IN
संबंधित प्रश्न
Find the area of the sector whose arc length and radius are 14 cm and 6 cm respectively.
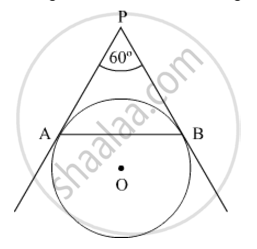
In Fig. 3, AP and BP are tangents to a circle with centre O, such that AP = 5 cm and ∠APB = 60°. Find the length of chord AB.
A chord of a circle of radius 15 cm subtends an angle of 60° at the centre. Find the areas of the corresponding minor and major segments of the circle. [Use π = 3.14 and `sqrt3 = 1.73`]
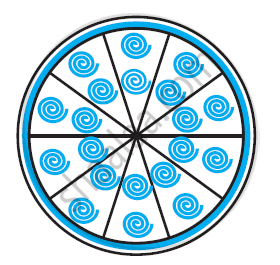
A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in figure. Find.
- The total length of the silver wire required.
- The area of each sector of the brooch [Use π = `22/7`]
To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships warned. [Use π = 3.14]
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`

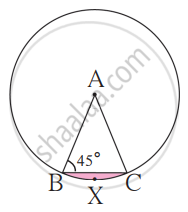
In the given figure, A is the center of the circle. ∠ABC = 45° and AC = 7√2 cm. Find the area of segment BXC.
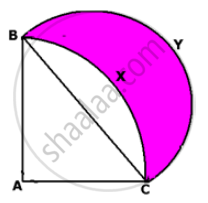
Choose the correct alternative answer for the following question.
Find the perimeter of a sector of a circle if its measure is 90° and radius is 7 cm.
A cow is tied with a rope of length 14 m at the corner of a rectangular field of dimensions 20 m × 16 m. Find the area of the field in which the cow can graze.
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the minor segment. [Use π = 3.14.]
A car has two wipers that do not overlap. Each wiper has a blade of length 21 cm sweeping through an angle of 120°. Find the total area cleaned at each sweep of the blades. `("Take" π =22/7)`
The area of the largest square that can be inscribed in a circle of radius 12 cm is ____________.
A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 7 m long rope. The area of that part of the field in which the horse can graze is ____________.
Find the area of the shaded region where ABC is a quadrant of radius 5cm and a semicircle is drawn with BC as diameter.
In figure, arcs are drawn by taking vertices A, B and C of an equilateral triangle of side 10 cm. to intersect the sides BC, CA and AB at their respective mid-points D, E and F. Find the area of the shaded region (Use π = 3.14).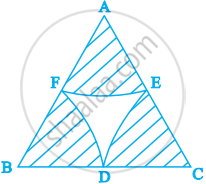
Sides of a triangular field are 15 m, 16 m and 17 m. With the three corners of the field a cow, a buffalo and a horse are tied separately with ropes of length 7 m each to graze in the field. Find the area of the field which cannot be grazed by the three animals.
Find the difference of the areas of a sector of angle 120° and its corresponding major sector of a circle of radius 21 cm.
The length of the arc of a circle of radius 14 cm which subtends an angle of 60° at the centre of the circle is ______.
Find the area of the sector of a circle of radius 7 cm and of central angle 90°. Also, find the area of corresponding major sector.
