Advertisements
Advertisements
प्रश्न
Find the difference of the areas of a sector of angle 120° and its corresponding major sector of a circle of radius 21 cm.
उत्तर
Given that, radius of the circle (r) = 21 cm and central angle of the sector AOBA (θ) = 120°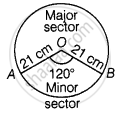
So, area of the circle
= πr2
= `22/7 xx (21)^2`
= `22/7 xx 21 xx 21`
= 22 × 3 × 21
= 1386 cm2
Now, area of the minor AOBA with central angle 120°
= `(pi"r"^2)/360^circ xx θ`
= `22/7 xx (21 xx 21)/360^circ xx 120`
= `(22 xx 3 xx 21)/3`
= 22 × 21
= 462 cm2
∴ Area of the major sector ABOA
= Area of the circle – Area of the sector AOBA
= 1386 – 462
= 924 cm2
∴ Difference of the areas of a sector AOBA and its corresponding major sector ABOA
= |Area of major sector ABOA – Area of minor sector AOBA|
= |924 – 462|
= 462 cm2
Hence, the required difference of two sectors is 462 cm2.
APPEARS IN
संबंधित प्रश्न
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes. [Use `pi = 22/7`]
Four cows are tethered at the four corners of a square field of side 50 m such that the each can graze the maximum unshared area. What area will be left ungrazed?
In following fig., ABCD is a square. A cirde is drawn with centre A so that it cuts AB and AD at Mand N respectively. Prove that Δ DAM ≅ Δ .BAN.
Find the area of a sector of a circle having radius 6 cm and length of the arc 15 cm.
Find the area of the sector of a circle of radius 8 cm and arc with length 15 cm.
The area of the largest square that can be inscribed in a circle of radius 12 cm is ____________.
A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 7 m long rope. The area of that part of the field in which the horse can graze is ____________.
Three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these circles.
Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14)
Given: The radius of a circle (r) = `square`
Measure of an arc of the circle (θ) = `square`
Area of the sector = `θ/360^circ xx square`
= `square/360^circ xx square xx square xx square`
= `square xx square xx square`
= 47.10 cm2
Find the area of the sector of a circle of radius 7 cm and of central angle 90°. Also, find the area of corresponding major sector.
