Advertisements
Advertisements
प्रश्न
Three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these circles.
उत्तर
Given that, three circles are in such a way that each of them touches the other two.
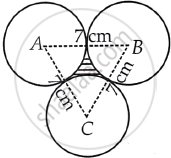
Now, join AB, BC and CA.
Since, radius of each circle is 3.5 cm.
So, AB = 2 × radius of circle
= 2 × 3.5 cm
= 7 cm
∴ AC = BC = AB = 7 cm
So, ΔABC is an equilateral triangle with side 7 cm.
We know that, each angle between two adjacent sides of an equilateral triangle is 60°.
∴ Area of sector with ∠A = 60°
= `(∠"A")/360^circ xx pi"r"^2`
= `60^circ/360^circ xx pi xx (3.5)^2 "cm"^2`
So, area of each sector = 3 × area of sector with angle A
= `3 xx 60^circ/360^circ xx pi xx (3.5)^2 "cm"^2`
= `1/2 xx 22/7 xx 3.5 xx 3.5 "cm"^2`
= `11 xx 5/10 xx 35/10 "cm"^2`
= `77/4 "cm"^2`
= 19.25 cm2
And area of ΔABC = `sqrt(3)/4 xx (7)^2 "cm"^2` ...[∵ Area of an equilateral triangle = `sqrt(3)/4 xx ("side")^2`]
= `(49sqrt(3))/4 "cm"^2`
∴ Area of shaded region enclosed between these circles
= Area of ΔABC – Area of each sector
= `(49sqrt(3))/4 - 19.25`
= `12.25 xx sqrt(3) - 19.25`
= 21.2176 – 19.25
= 1.9676 cm2
Hence, the required area enclosed between these circles is 1.967 cm2 (approx).
APPEARS IN
संबंधित प्रश्न
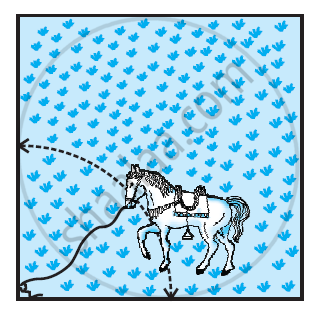
A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see the given figure). Find
- The area of that part of the field in which the horse can graze.
- The increase in the grazing area of the rope were 10 m long instead of 5 m. [Use π = 3.14]
Area of a sector of angle p (in degrees) of a circle with radius R is ______.
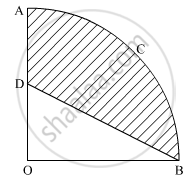
In the given figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the shaded region.
A sector is cut-off from a circle of radius 21 cm the angle of sector is 120°. Find the length of its arc and its area.
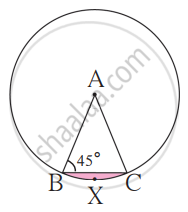
In the given figure, A is the center of the circle. ∠ABC = 45° and AC = 7√2 cm. Find the area of segment BXC.
The length of the minute hand of a clock is 5 cm. Find the area swept by the minute hand during the time period 6 : 05 am and 6 : 40 am.
A chord 10 cm long is drawn in a circle whose radius is `5sqrt(2)` cm. Find the areas of both the segments.
A car has two wipers that do not overlap. Each wiper has a blade of length 21 cm sweeping through an angle of 120°. Find the total area cleaned at each sweep of the blades. `("Take" π =22/7)`
Find the area of a sector of a circle of radius 28 cm and central angle 45°.
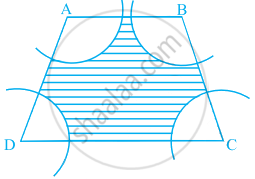
In figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and distance between AB and DC = 14 cm. If arcs of equal radii 7 cm with centres A, B, C and D have been drawn, then find the area of the shaded region of the figure.