Advertisements
Advertisements
Question
Three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these circles.
Solution
Given that, three circles are in such a way that each of them touches the other two.
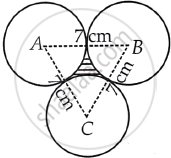
Now, join AB, BC and CA.
Since, radius of each circle is 3.5 cm.
So, AB = 2 × radius of circle
= 2 × 3.5 cm
= 7 cm
∴ AC = BC = AB = 7 cm
So, ΔABC is an equilateral triangle with side 7 cm.
We know that, each angle between two adjacent sides of an equilateral triangle is 60°.
∴ Area of sector with ∠A = 60°
= `(∠"A")/360^circ xx pi"r"^2`
= `60^circ/360^circ xx pi xx (3.5)^2 "cm"^2`
So, area of each sector = 3 × area of sector with angle A
= `3 xx 60^circ/360^circ xx pi xx (3.5)^2 "cm"^2`
= `1/2 xx 22/7 xx 3.5 xx 3.5 "cm"^2`
= `11 xx 5/10 xx 35/10 "cm"^2`
= `77/4 "cm"^2`
= 19.25 cm2
And area of ΔABC = `sqrt(3)/4 xx (7)^2 "cm"^2` ...[∵ Area of an equilateral triangle = `sqrt(3)/4 xx ("side")^2`]
= `(49sqrt(3))/4 "cm"^2`
∴ Area of shaded region enclosed between these circles
= Area of ΔABC – Area of each sector
= `(49sqrt(3))/4 - 19.25`
= `12.25 xx sqrt(3) - 19.25`
= 21.2176 – 19.25
= 1.9676 cm2
Hence, the required area enclosed between these circles is 1.967 cm2 (approx).
APPEARS IN
RELATED QUESTIONS
In a circle of radius 35 cm, an arc subtends an angle of 72° at the centre. Find the length of arc and area of sector
A chord of a circle subtends an angle 𝜃 at the centre of circle. The area of the minor segment cut off by the chord is one eighth of the area of circle. Prove that 8 sin`theta/2 "cos"theta/2+pi =(pitheta)/45`
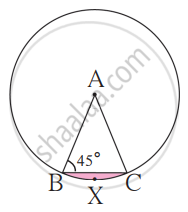
In the given figure, A is the center of the circle. ∠ABC = 45° and AC = 7√2 cm. Find the area of segment BXC.
In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

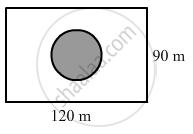
A park is in the form of a rectangle 120 m by 90 m. At the centre of the park there is a circular lawn as shown in the figure. The area of the park excluding the lawn is 2950 m2. Find the radius of the circular lawn.
In following figure , C is a point on the minor arc AB of the circle with centre O . Given ∠ ACB = p° , ∠ AOB = q° , express q in terms of p. Calculate p if OACB is a parallelogram.

In the following figure, if m(arc DXE) = 120° and m(arc AYC) = 60°. Find ∠DBE.

If `theta` is the angle in degrees of a sector of a circle of radius V, then area of the sector is ____________.
If the length of an arc of a circle of radius r is equal to that of an arc of a circle of radius 2r, then the angle of the corresponding sector of the first circle is double the angle of the corresponding sector of the other circle. Is this statement false? Why?
The number of revolutions made by a circular wheel of radius 0.25 m in rolling a distance of 11 km is ______.
