Advertisements
Advertisements
Question
A park is in the form of a rectangle 120 m by 90 m. At the centre of the park there is a circular lawn as shown in the figure. The area of the park excluding the lawn is 2950 m2. Find the radius of the circular lawn.
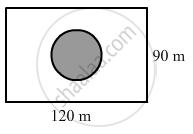
Solution
Area of the rectangle = l × b
= 120 × 90
= 10800 sq. m
Area of the park excluding the lawn = 2950 m2
Area of the circular lawn = Area of the park -- Area of the park excluding the lawn
= 10800 - 2950
= 7850 m2
Area of the circular lawn =πr2
`=> 7850 = 22/7xx"r"^2`
`=> (7850) = 22/7xx"r"^2`
`=> "r"^2 = 2497.72`
⇒ r = 49.97
Or,
r ≈ 50 m
Thus, the radius of the circular lawn is 50 m.
APPEARS IN
RELATED QUESTIONS
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes. [Use `pi = 22/7`]
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm and divides the circle into two segments. Find the area of the minor segment.
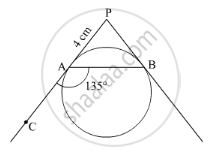
In the given figure, PA and PB are tangents to a circle from an external point P such that PA = 4 cm and ∠BAC = 135°. Find the length of chord AB ?
The length of the minute hand of a clock is 5 cm. Find the area swept by the minute hand during the time period 6 : 05 am and 6 : 40 am.
In the given figure, APB and CQD are semicircles of diameter 7 cm each, while ARC an BSD are semicircles of diameter 14 cm each. Find the
- perimeter
- area of the shaded region.
Four cows are tethered at the four corners of a square field of side 50 m such that the each can graze the maximum unshared area. What area will be left ungrazed?
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
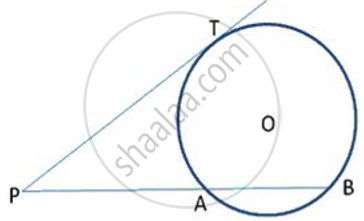
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
In figure, arcs have been drawn of radius 21 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.
Is it true to say that area of a segment of a circle is less than the area of its corresponding sector? Why?
