Advertisements
Advertisements
Question
In the given figure, PA and PB are tangents to a circle from an external point P such that PA = 4 cm and ∠BAC = 135°. Find the length of chord AB ?
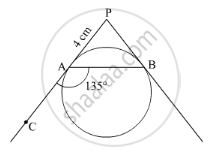
Solution
It is given that PA and PB are tangents drawn from an external point P to the circle.
∴ PA = PB = 4 cm (Lengths of tangents drawn from an external point to a circle are equal)
Also, \[\angle BAC = 135^o\]
Now,
\[ \Rightarrow \angle PAB = 180^o - 135^o = 45^0\]
∴ \[\angle PBA = \angle PAB = 45^o\] (In a triangle, equal sides have equal angles opposite to them)
Also,
\[ \Rightarrow \angle APB = 180^o - 90^o = 90^o\]
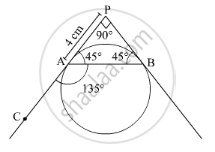
\[ \Rightarrow AB = \sqrt{\left( 4 \right)^2 + \left( 4 \right)^2} = \sqrt{32} = 4\sqrt{2} cm\]
APPEARS IN
RELATED QUESTIONS
Find the area of the sector whose arc length and radius are 14 cm and 6 cm respectively.
The area of sector of circle of radius 5cm is 5𝜋 cm2. Find the angle contained by the sector.
A sector is cut-off from a circle of radius 21 cm the angle of sector is 120°. Find the length of its arc and its area.
A chord 10 cm long is drawn in a circle whose radius is 5√2 cm. Find the area of both
segments
The radius of a circle is 10 cm. The area of a sector of the sector is 100 cm2. Find the area of its corresponding major sector. ( \[\pi\] = 3.14 ).
In the given figure, if O is the center of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of the shaded region is 114 cm2, find the radius of the circle. \[\pi\] = 3.14)

Find the area of a sector of a circle having radius 6 cm and length of the arc 15 cm.
If the length of an arc of a circle of radius r is equal to that of an arc of a circle of radius 2r, then the angle of the corresponding sector of the first circle is double the angle of the corresponding sector of the other circle. Is this statement false? Why?
The areas of two sectors of two different circles with equal corresponding arc lengths are equal. Is this statement true? Why?
The length of the minute hand of a clock is 6 cm. Find the area swept by it when it moves from 7:05 p.m. to 7:40 p.m.
