Advertisements
Advertisements
प्रश्न
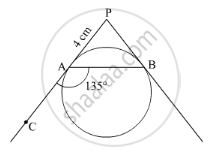
In the given figure, PA and PB are tangents to a circle from an external point P such that PA = 4 cm and ∠BAC = 135°. Find the length of chord AB ?
उत्तर
It is given that PA and PB are tangents drawn from an external point P to the circle.
∴ PA = PB = 4 cm (Lengths of tangents drawn from an external point to a circle are equal)
Also, \[\angle BAC = 135^o\]
Now,
\[ \Rightarrow \angle PAB = 180^o - 135^o = 45^0\]
∴ \[\angle PBA = \angle PAB = 45^o\] (In a triangle, equal sides have equal angles opposite to them)
Also,
\[ \Rightarrow \angle APB = 180^o - 90^o = 90^o\]
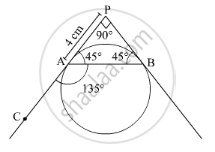
\[ \Rightarrow AB = \sqrt{\left( 4 \right)^2 + \left( 4 \right)^2} = \sqrt{32} = 4\sqrt{2} cm\]
APPEARS IN
संबंधित प्रश्न
Find the area of the minor segment of a circle of radius 14 cm, when its central angle is 60˚. Also find the area of the corresponding major segment.[use π=22/7]
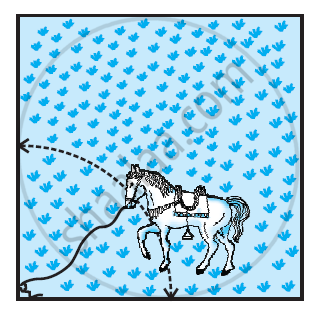
A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see the given figure). Find
- The area of that part of the field in which the horse can graze.
- The increase in the grazing area of the rope were 10 m long instead of 5 m. [Use π = 3.14]
Area of a sector of angle p (in degrees) of a circle with radius R is ______.
Choose the correct alternative answer for the following question.
Find the perimeter of a sector of a circle if its measure is 90° and radius is 7 cm.
The radius of a circle is 17.5 cm. Find the area of the sector enclosed by two radii and an arc 44 cm in length.
Find the area of the sector whose arc length and radius are 8 cm and 3 cm respectively.
Find the area of a sector of a circle of radius 28 cm and central angle 45°.
The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
The number of revolutions made by a circular wheel of radius 0.25 m in rolling a distance of 11 km is ______.
With vertices A, B and C of ΔABC as centres, arcs are drawn with radii 14 cm and the three portions of the triangle so obtained are removed. Find the total area removed from the triangle.
