Advertisements
Advertisements
प्रश्न
A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see the given figure). Find
- The area of that part of the field in which the horse can graze.
- The increase in the grazing area of the rope were 10 m long instead of 5 m. [Use π = 3.14]
उत्तर
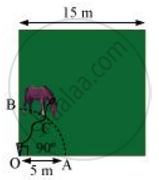
i) From the figure, it can be observed that the horse can graze a sector of 90° in a circle of 5 m radius.
Area that can be grazed by horse = Area of sector OACB
`= (90^@)/360^@ pir^2`
`=1/4xx 3.14xx (5)^2`
= 19.625 m2
ii) Area that can be grazed by the horse when length of rope is 10 m long
`=(90^@)/(360^@) xx pi xx (10)^2 `
=`1/4 xx 3.14 xx 100`
= 78.5 m2
Increase in grazing area = (78.5 − 19.625) m2
= 58.875 m2
APPEARS IN
संबंधित प्रश्न
Find the area of the sector whose arc length and radius are 14 cm and 6 cm respectively.
Find the area of a quadrant of a circle whose circumference is 22 cm. [Use `pi = 22/7`]
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes. [Use `pi = 22/7`]
A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle. [Use π = 3.14 and `sqrt3 = 1.73` ]
A sector of a circle of radius 8cm contains the angle of 135°. Find the area of sector.
A sector of 56° cut out from a circle contains area of 4.4 cm2. Find the radius of the circle
A chord of a circle subtends an angle 𝜃 at the centre of circle. The area of the minor segment cut off by the chord is one eighth of the area of circle. Prove that 8 sin`theta/2 "cos"theta/2+pi =(pitheta)/45`
In the given figure, O is the centre of the circle. m ( arc PQR) = 60° OP = 10 cm. Find the area of the shaded region.( \[\pi\]= 3.14, \[\sqrt{3}\]= 1.73)

A cow is tied with a rope of length 14 m at the corner of a rectangular field of dimensions 20 m × 16 m. Find the area of the field in which the cow can graze.
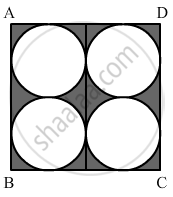
In the given figure, find the area of the shaded region, where ABCD is a square of side 14 cm and all circles are of the same diameter.
Four cows are tethered at the four corners of a square field of side 50 m such that each can graze the maximum unshared area. What area will be left ungrazed?
In following figure , C is a point on the minor arc AB of the circle with centre O . Given ∠ ACB = p° , ∠ AOB = q° , express q in terms of p. Calculate p if OACB is a parallelogram.

The diameter of a sphere is 6 cm, Find the total surface area of the sphere. (π = 3.14)
A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 7 m long rope. The area of that part of the field in which the horse can graze is ____________.
In figure, arcs have been drawn of radius 21 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.
In figure, arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region.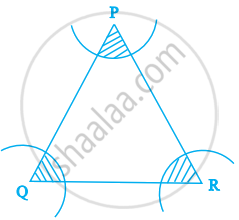
Three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these circles.
Find the area of the sector of a circle of radius 5 cm, if the corresponding arc length is 3.5 cm.
Four circular cardboard pieces of radii 7 cm are placed on a paper in such a way that each piece touches other two pieces. Find the area of the portion enclosed between these pieces.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the segment formed by the corresponding chord. (Use π = `22/7`)
