Advertisements
Advertisements
प्रश्न
In figure, arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region.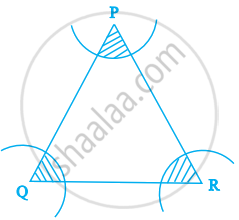
उत्तर
Given that, radii of each arc (r) = 14 cm
Now, area of the sector with central angle P
= `(∠"P")/360^circ xx π"r"^2`
= `(∠"P")/360^circ xx π xx (14)^2 "cm"^2`
Area of the sector with central angle Q
= `(∠"Q")/360^circ xx π"r"^2`
= `(∠"Q")/360^circ xx π xx (14)^2 "cm"^2`
And area of the sector with central angle R
= `(∠"R")/360^circ xx π"r"^2`
= `(∠"R")/360^circ xx π xx (14)^2 "cm"^2`
Therefore, sum of the areas of three sectors
= `(∠"P")/360^circ xx π xx (14)^2 + (∠"Q")/360^circ xx π xx (14)^2 + (∠"R")/360^circ xx π xx (14)^2`
= `π/360^circ xx (14)^2 xx [∠"P" + ∠"Q" + ∠"R"]`
= `π/360^circ xx 196 xx 180^circ` ...[Since, sum of all interior angles in any triangle is 180°]
= 98π
= `98 xx 22/7`
= 14 × 22
= 308
Hence, the required area of the shaded region is 308 cm2.
APPEARS IN
संबंधित प्रश्न
A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle. [Use π = 3.14 and `sqrt3 = 1.73` ]
The area of sector of circle of radius 5cm is 5𝜋 cm2. Find the angle contained by the sector.
A sector of 56° cut out from a circle contains area of 4.4 cm2. Find the radius of the circle
In the given figure, ABCD is a square of side 7 cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.

In the given figure, find the area of the shaded region, where ABCD is a square of side 14 cm and all circles are of the same diameter.
Find the area of the sector whose arc length and radius are 8 cm and 3 cm respectively.
The diameter of a sphere is 6 cm, Find the total surface area of the sphere. (π = 3.14)
Find the area of the minor segment of a circle of radius 14 cm, when the angle of the corresponding sector is 60°.
Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14)
Given: The radius of a circle (r) = `square`
Measure of an arc of the circle (θ) = `square`
Area of the sector = `θ/360^circ xx square`
= `square/360^circ xx square xx square xx square`
= `square xx square xx square`
= 47.10 cm2
The length of the minute hand of a clock is 6 cm. Find the area swept by it when it moves from 7:05 p.m. to 7:40 p.m.
