Advertisements
Advertisements
प्रश्न
Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14)
Given: The radius of a circle (r) = `square`
Measure of an arc of the circle (θ) = `square`
Area of the sector = `θ/360^circ xx square`
= `square/360^circ xx square xx square xx square`
= `square xx square xx square`
= 47.10 cm2
उत्तर
Given: The radius of a circle (r) = 10 cm
Measure of an arc of the circle (θ) = 54°
Area of the sector = `θ/360^circ` × πr2
= `bb54/360^circ` × 3.14 × 10 × 10
= 3 × 1.57 × 10
= 47.10 cm2
APPEARS IN
संबंधित प्रश्न
Area of a sector of angle p (in degrees) of a circle with radius R is ______.
The diagram shows a sector of circle of radius ‘r’ can containing an angle 𝜃. The area of sector is A cm2 and perimeter of sector is 50 cm. Prove that
(i) 𝜃 =`360/pi(25/r− 1)`
(ii) A = 25r – r2
A chord AB of circle, of radius 14cm makes an angle of 60° at the centre. Find the area of minor segment of circle.
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`
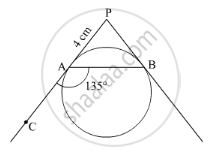
In the given figure, PA and PB are tangents to a circle from an external point P such that PA = 4 cm and ∠BAC = 135°. Find the length of chord AB ?
(2) Area of any one of the sectors
Area of a sector of central angle 200° of a circle is 770 cm2. Find the length of the corresponding arc of this sector.
A cow is tied with a rope of length 14 m at the corner of a rectangular field of dimensions 20 m × 16 m. Find the area of the field in which the cow can graze.
In the given figure, APB and CQD are semicircles of diameter 7 cm each, while ARC an BSD are semicircles of diameter 14 cm each. Find the
- perimeter
- area of the shaded region.
If angle of sector is 60°, radius is 3.5 cm then length of the arc is ____________.
A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 7 m long rope. The area of that part of the field in which the horse can graze is ____________.
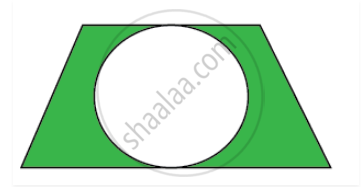
In the given figure, a circle is inscribed in a trapezium of height 14 cm and lengths of parallel sides are equal to 25 cm and 40 cm. What is the area of the shaded region?
If the length of an arc of a circle of radius r is equal to that of an arc of a circle of radius 2r, then the angle of the corresponding sector of the first circle is double the angle of the corresponding sector of the other circle. Is this statement false? Why?
The areas of two sectors of two different circles with equal corresponding arc lengths are equal. Is this statement true? Why?
In figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and distance between AB and DC = 14 cm. If arcs of equal radii 7 cm with centres A, B, C and D have been drawn, then find the area of the shaded region of the figure.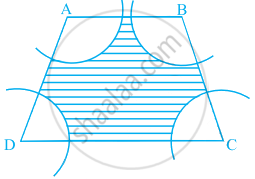
Find the area of the sector of a circle of radius 5 cm, if the corresponding arc length is 3.5 cm.
The number of revolutions made by a circular wheel of radius 0.25 m in rolling a distance of 11 km is ______.
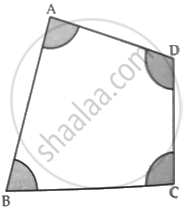
In the given figure, arcs have been drawn of radius 7 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the segment formed by the corresponding chord. (Use π = `22/7`)
