Advertisements
Advertisements
प्रश्न
A chord AB of circle, of radius 14cm makes an angle of 60° at the centre. Find the area of minor segment of circle.
उत्तर
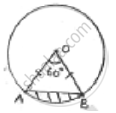
Given radius (r) = 14cm = OA = OB
𝜃 = angle at centre = 60°
In ΔAOB, ∠A = ∠B [angles opposite to equal sides OA and OB] = x
By angle sum property ∠A + ∠B + ∠O = 180°
x + x + 60° = 180° ⇒ 2x = 120° ⇒ x = 60°
All angles are 60°, OAB is equilateral OA = OB = AB
Area of segment = area of sector – area Δle OAB
=`theta/360^@× pir^2 − sqrt(3)/4× (−AB)^2`
=`60/360×22/7× 14 × 14 − sqrt(3)/4× 14 × 14`
=`308/3− 49sqrt(3)`
`= (308−147sqrt(3))/3cm^2`
APPEARS IN
संबंधित प्रश्न
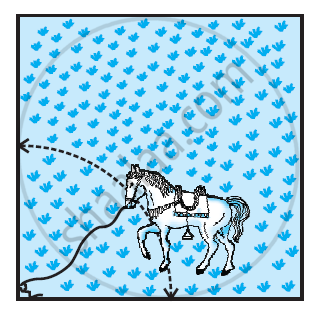
A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see the given figure). Find
- The area of that part of the field in which the horse can graze.
- The increase in the grazing area of the rope were 10 m long instead of 5 m. [Use π = 3.14]
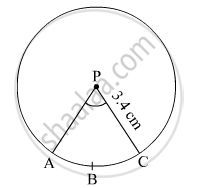
In the given figure, radius of circle is 3.4 cm and perimeter of sector P-ABC is 12.8 cm . Find A(P-ABC).
A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 7 m long rope. The area of that part of the field in which the horse can graze is ____________.
Find the area of the minor segment of a circle of radius 14 cm, when the angle of the corresponding sector is 60°.
Find the area of the segment of a circle of radius 12 cm whose corresponding sector has a central angle of 60° (Use π = 3.14).
Three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these circles.
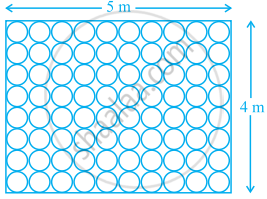
Floor of a room is of dimensions 5 m × 4 m and it is covered with circular tiles of diameters 50 cm each as shown in figure. Find the area of floor that remains uncovered with tiles. (Use π = 3.14)
Find the perimeter of a quadrant of a circle of radius 14 cm.
What is the length of arc of a circle of radius 7 cm which subtends an angle of 90° at the centre of the circle?
The area of the sector of a circle of radius 12 cm is 60π cm2. The central angle of this sector is ______.
