Advertisements
Advertisements
प्रश्न
Find the area of the minor segment of a circle of radius 14 cm, when the angle of the corresponding sector is 60°.
उत्तर
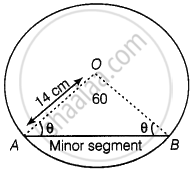
Given that, radius of circle (r) = 14 cm
And angle of the corresponding sector i.e., central angle (θ) = 60°
Since, in ΔAOB, OA = OB = Radius of circle i.e., ΔAOB is isosceles.
⇒ ∠OAB = ∠OBA = θ
Now, in ΔOAB,
∠AOB + ∠OAB = ∠OBA = 180° ...[Since, sum of interior angles of any triangle is 180°]
⇒ 60° + θ + θ = 180° ...[Given, ∠AOB = 60°]
⇒ 2θ = 120°
⇒ θ = 60°
i.e. ∠OAB = ∠OBA = 60° = ∠AOB
Since, all angles of ΔAOB are equal to 60° i.e., ΔAOB is an equilateral triangle.
Also, OA = OB = AB = 14 cm
So, Area of ΔOAB = `sqrt(3)/4` (side)2
= `sqrt(3)/4 xx (14)^2` ...[∵ Area of an equilateral triangle = `sqrt(3)/4` (sides)2]
= `sqrt(3)/4 xx 196`
= `49sqrt(3) "cm"^2`
APPEARS IN
संबंधित प्रश्न
A round table cover has six equal designs, as shown in figure. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs.0.35 per cm2. [Use `sqrt3 = 1.7`]
In fig. 6, AB is a chord of a circle, with centre O, such that AB = 16 cm and radius of circle is 10 cm. Tangents at A and B intersect each other at P. Find the length of PA ?

(2) Area of any one of the sectors
A chord PQ of a circle with a radius of cm subtends an angle of 60° with the center of the circle. Find the area of the minor as well as the major segment. ( \[\pi\] = 3.14, \[\sqrt{3}\] = 1.73)
In the following figure, if m(arc DXE) = 120° and m(arc AYC) = 60°. Find ∠DBE.

Sides of a triangular field are 15 m, 16 m and 17 m. With the three corners of the field a cow, a buffalo and a horse are tied separately with ropes of length 7 m each to graze in the field. Find the area of the field which cannot be grazed by the three animals.
Find the area of the sector of a circle of radius 5 cm, if the corresponding arc length is 3.5 cm.
The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
The number of revolutions made by a circular wheel of radius 0.25 m in rolling a distance of 11 km is ______.
With vertices A, B and C of ΔABC as centres, arcs are drawn with radii 14 cm and the three portions of the triangle so obtained are removed. Find the total area removed from the triangle.
