Advertisements
Advertisements
प्रश्न
Find the area of the minor segment of a circle of radius 14 cm, when the angle of the corresponding sector is 60°.
उत्तर
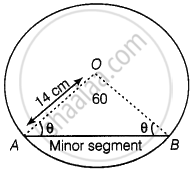
Given that, radius of circle (r) = 14 cm
And angle of the corresponding sector i.e., central angle (θ) = 60°
Since, in ΔAOB, OA = OB = Radius of circle i.e., ΔAOB is isosceles.
⇒ ∠OAB = ∠OBA = θ
Now, in ΔOAB,
∠AOB + ∠OAB = ∠OBA = 180° ...[Since, sum of interior angles of any triangle is 180°]
⇒ 60° + θ + θ = 180° ...[Given, ∠AOB = 60°]
⇒ 2θ = 120°
⇒ θ = 60°
i.e. ∠OAB = ∠OBA = 60° = ∠AOB
Since, all angles of ΔAOB are equal to 60° i.e., ΔAOB is an equilateral triangle.
Also, OA = OB = AB = 14 cm
So, Area of ΔOAB = `sqrt(3)/4` (side)2
= `sqrt(3)/4 xx (14)^2` ...[∵ Area of an equilateral triangle = `sqrt(3)/4` (sides)2]
= `sqrt(3)/4 xx 196`
= `49sqrt(3) "cm"^2`
APPEARS IN
संबंधित प्रश्न
In Fig. 3, AP and BP are tangents to a circle with centre O, such that AP = 5 cm and ∠APB = 60°. Find the length of chord AB.
Find the area of a quadrant of a circle whose circumference is 22 cm. [Use `pi = 22/7`]
A sector of circle of radius 4cm contains an angle of 30°. Find the area of sector

Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
In following figure , C is a point on the minor arc AB of the circle with centre O . Given ∠ ACB = p° , ∠ AOB = q° , express q in terms of p. Calculate p if OACB is a parallelogram.

If the length of an arc of a circle of radius r is equal to that of an arc of a circle of radius 2r, then the angle of the corresponding sector of the first circle is double the angle of the corresponding sector of the other circle. Is this statement false? Why?
Find the difference of the areas of a sector of angle 120° and its corresponding major sector of a circle of radius 21 cm.
The length of the minute hand of a clock is 6 cm. Find the area swept by it when it moves from 7:05 p.m. to 7:40 p.m.
What is the length of arc of a circle of radius 7 cm which subtends an angle of 90° at the centre of the circle?
