Advertisements
Advertisements
प्रश्न
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
उत्तर
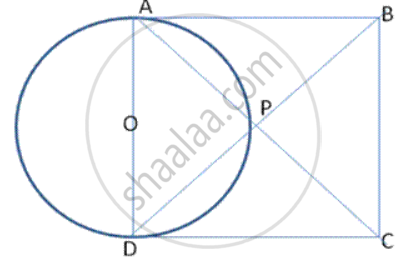
We know that the diagonals of a rhombus bisect each other at right angles.
∴ ∠ APO =90° - (1)
Also, AD is the diameter of the circle with centre 0
∴ ∠ APD=90° - (2) (Angle in semi circle)
From ( 1) and (2), we get, The cirde drawn with any side of a rhombus as a diameter, passes through point of intersection of its diagonals.
APPEARS IN
संबंधित प्रश्न
Find the area of the sector whose arc length and radius are 14 cm and 6 cm respectively.
A sector of a circle of radius 8cm contains the angle of 135°. Find the area of sector.
The diagram shows a sector of circle of radius ‘r’ can containing an angle 𝜃. The area of sector is A cm2 and perimeter of sector is 50 cm. Prove that
(i) 𝜃 =`360/pi(25/r− 1)`
(ii) A = 25r – r2
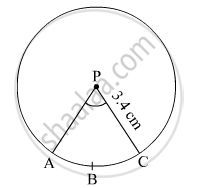
In the given figure, radius of circle is 3.4 cm and perimeter of sector P-ABC is 12.8 cm . Find A(P-ABC).
In the given figure, ABCD is a square of side 7 cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.

If angle of sector is 60°, radius is 3.5 cm then length of the arc is ____________.
In figure, arcs have been drawn of radius 21 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.
In figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and distance between AB and DC = 14 cm. If arcs of equal radii 7 cm with centres A, B, C and D have been drawn, then find the area of the shaded region of the figure.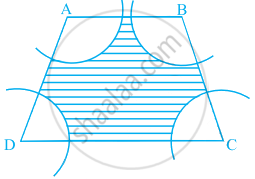
The length of the minute hand of a clock is 6 cm. Find the area swept by it when it moves from 7:05 p.m. to 7:40 p.m.
With vertices A, B and C of ΔABC as centres, arcs are drawn with radii 14 cm and the three portions of the triangle so obtained are removed. Find the total area removed from the triangle.
