Advertisements
Advertisements
प्रश्न
The diagram shows a sector of circle of radius ‘r’ can containing an angle 𝜃. The area of sector is A cm2 and perimeter of sector is 50 cm. Prove that
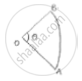
(i) 𝜃 =`360/pi(25/r− 1)`
(ii) A = 25r – r2
उत्तर
(i) Radius of circle = ‘r’ cm
Angle subtended at centre = 𝜃
Perimeter = OA + OB + (AB arc)
= r + r +`theta/360^@× 2pir = 2r + 2r [(pitheta)/360^@]`
But perimeter given as 50
`50 = 2r [1 +(pitheta)/360^@]`
⇒`(pitheta)/360^@=50/(2r)− 1`
⇒ 𝜃 =`360^@/pi[25/r− 1]` …..(i)
(ii) Area of sector =`theta/360^@× pir^2`
=`((360^@/pi)(25/r−1))/360^@× pir^2`
=`25/r× r^2 − r^2`
= 25r – r2
⇒ A = 25r – r2 …..(ii)
APPEARS IN
संबंधित प्रश्न
Find the area of sector whose arc length and radius are 10 cm and 5 cm respectively
A chord of a circle of radius 15 cm subtends an angle of 60° at the centre. Find the areas of the corresponding minor and major segments of the circle. [Use π = 3.14 and `sqrt3 = 1.73`]
The perimeter of certain sector of circle of radius 5.6 m is 27.2 m. Find the area of sector.
In the given figure, if A is the centre of the circle. \[\angle\] PAR = 30°, AP = 7.5, find the area of the segment PQR. (\[\pi\] = 3.14)

A chord PQ of a circle with a radius of cm subtends an angle of 60° with the center of the circle. Find the area of the minor as well as the major segment. ( \[\pi\] = 3.14, \[\sqrt{3}\] = 1.73)
In the given figure, ABCD is a square of side 7 cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.

In following figure , C is a point on the minor arc AB of the circle with centre O . Given ∠ ACB = p° , ∠ AOB = q° , express q in terms of p. Calculate p if OACB is a parallelogram.

In figure, arcs are drawn by taking vertices A, B and C of an equilateral triangle of side 10 cm. to intersect the sides BC, CA and AB at their respective mid-points D, E and F. Find the area of the shaded region (Use π = 3.14).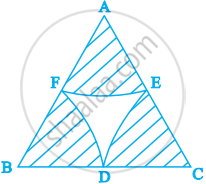
Find the area of the unshaded region shown in the given figure.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the segment formed by the corresponding chord. (Use π = `22/7`)
