Advertisements
Advertisements
प्रश्न
A chord of a circle of radius 15 cm subtends an angle of 60° at the centre. Find the areas of the corresponding minor and major segments of the circle. [Use π = 3.14 and `sqrt3 = 1.73`]
उत्तर
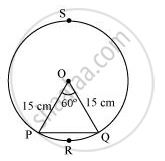
Radius (r) of circle = 15 cm
Area of sector OPRQ = `60^@/360^@xxpir^2`
= `1/6 xx 3.14 xx (15)^2`
= 117.75 cm2
In ΔOPQ,
∠OPQ = ∠OQP (As OP = OQ)
∠OPQ + ∠OQP + ∠POQ = 180°
2 ∠OPQ = 120°
∠OPQ = 60°
ΔOPQ is an equilateral triangle.
Area of ΔOPQ = `(sqrt3)/4 xx (r)^2`
`= sqrt3/4 xx (15)^2`
= `(225sqrt3)/4 "cm"^2`
`= 56.25sqrt3`
97.3125 cm2
Area of segment PRQ = Area of sector OPRQ − Area of ΔOPQ
= 117.75 − 97.3125
= 20.4375 cm2
Area of major segment PSQ = Area of circle − Area of segment PRQ
= πr2 − 20.4375
= π × (15)2 − 20.4375
= 3.14 × 225 − 20.4375
= 706.5 − 20.4375
= 686.0625 cm2
APPEARS IN
संबंधित प्रश्न
Find the area of sector whose arc length and radius are 10 cm and 5 cm respectively
A car has two wipers which do not overlap. Each wiper has blade of length 25 cm sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades [Use π = `22/7`]
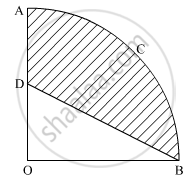
In the given figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the shaded region.
The area of sector of circle of radius 5cm is 5𝜋 cm2. Find the angle contained by the sector.
The diagram shows a sector of circle of radius ‘r’ can containing an angle 𝜃. The area of sector is A cm2 and perimeter of sector is 50 cm. Prove that
(i) 𝜃 =`360/pi(25/r− 1)`
(ii) A = 25r – r2
A chord of circle of radius 14cm makes a right angle at the centre. Find the areas of minor and major segments of the circle.
In the given figure, O is the centre of the circle. m ( arc PQR) = 60° OP = 10 cm. Find the area of the shaded region.( \[\pi\]= 3.14, \[\sqrt{3}\]= 1.73)

In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

In the given figure, if O is the center of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of the shaded region is 114 cm2, find the radius of the circle. \[\pi\] = 3.14)

Area of a sector of central angle 200° of a circle is 770 cm2. Find the length of the corresponding arc of this sector.
The radius of a circle is 17.5 cm. Find the area of the sector enclosed by two radii and an arc 44 cm in length.
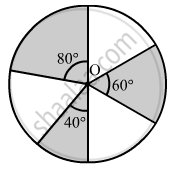
In the given figure, three sectors of a circle of radius 7 cm, making angles of 60°, 80° and 40° at the centre are shaded. Find the area of the shaded region.
A chord 10 cm long is drawn in a circle whose radius is `5sqrt(2)` cm. Find the areas of both the segments.
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
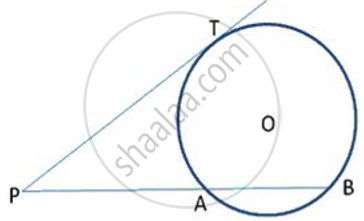
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
Find the area of the sector whose arc length and radius are 8 cm and 3 cm respectively.
In the following figure, if m(arc DXE) = 120° and m(arc AYC) = 60°. Find ∠DBE.

In figure, arcs have been drawn of radius 21 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.
The number of revolutions made by a circular wheel of radius 0.25 m in rolling a distance of 11 km is ______.
