Advertisements
Advertisements
рдкреНрд░рд╢реНрди
A chord of circle of radius 14cm makes a right angle at the centre. Find the areas of minor and major segments of the circle.
рдЙрддреНрддрд░
Radius (r) = 14cm
ЁЭЬГ = 90°
= OA = OB
Area of minor segment (ANB)
= (ЁЭСОЁЭСЯЁЭСТЁЭСО ЁЭСЬЁЭСУ ЁЭР┤ЁЭСБЁЭР╡ ЁЭСаЁЭСТЁЭСРЁЭСбЁЭСЬЁЭСЯ) − (ЁЭСОЁЭСЯЁЭСТЁЭСО ЁЭСЬЁЭСУ ΔЁЭР┤ЁЭСВЁЭР╡)
=`theta/360^@× pir^2 −1/2`× ЁЭСВЁЭР┤ × ЁЭСВЁЭР╡
=`90/360×22/7× 14 × 14 −1/2× 14 × 14`
= 154 − 98 = 56ЁЭСРЁЭСЪ2
Area of major segment (other than shaded)
= area of circle – area of segment ANB
= ЁЭЬЛЁЭСЯ2 − 56
=`22/7`× 14 × 14 − 56
= 616 – 56
= 560 cm2.
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНтАНрди
Area of a sector of angle p (in degrees) of a circle with radius R is ______.
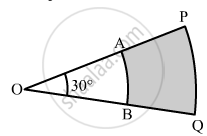
In the given figure, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and 3.5 cm with centre O. If ∠POQ = 30°, find the area of the shaded region.
In following figure , C is a point on the minor arc AB of the circle with centre O . Given ∠ ACB = p° , ∠ AOB = q° , express q in terms of p. Calculate p if OACB is a parallelogram.
A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 7 m long rope. The area of that part of the field in which the horse can graze is ____________.
The number of revolutions made by a circular wheel of radius 0.7m in rolling a distance of 176m is ______.
In figure, arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region.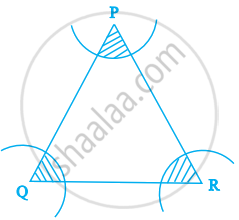
Find the difference of the areas of a sector of angle 120° and its corresponding major sector of a circle of radius 21 cm.
Find the perimeter of a quadrant of a circle of radius 14 cm.
What is the length of arc of a circle of radius 7 cm which subtends an angle of 90° at the centre of the circle?
With vertices A, B and C of ΔABC as centres, arcs are drawn with radii 14 cm and the three portions of the triangle so obtained are removed. Find the total area removed from the triangle.
