Advertisements
Advertisements
प्रश्न
A chord of circle of radius 14cm makes a right angle at the centre. Find the areas of minor and major segments of the circle.
उत्तर

Radius (r) = 14cm
𝜃 = 90°
= OA = OB
Area of minor segment (ANB)
= (𝑎𝑟𝑒𝑎 𝑜𝑓 𝐴𝑁𝐵 𝑠𝑒𝑐𝑡𝑜𝑟) − (𝑎𝑟𝑒𝑎 𝑜𝑓 Δ𝐴𝑂𝐵)
=`theta/360^@× pir^2 −1/2`× 𝑂𝐴 × 𝑂𝐵
=`90/360×22/7× 14 × 14 −1/2× 14 × 14`
= 154 − 98 = 56𝑐𝑚2
Area of major segment (other than shaded)
= area of circle – area of segment ANB
= 𝜋𝑟2 − 56
=`22/7`× 14 × 14 − 56
= 616 – 56
= 560 cm2.
APPEARS IN
संबंधित प्रश्न
The perimeter of a sector of circle of radius 5.7m is 27.2 m. Find the area of sector.
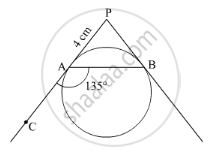
In the given figure, PA and PB are tangents to a circle from an external point P such that PA = 4 cm and ∠BAC = 135°. Find the length of chord AB ?
In fig. 6, AB is a chord of a circle, with centre O, such that AB = 16 cm and radius of circle is 10 cm. Tangents at A and B intersect each other at P. Find the length of PA ?

A cow is tied with a rope of length 14 m at the corner of a rectangular field of dimensions 20 m × 16 m. Find the area of the field in which the cow can graze.
A chord 10 cm long is drawn in a circle whose radius is `5sqrt(2)` cm. Find the areas of both the segments.
Find the area of the sector whose arc length and radius are 8 cm and 3 cm respectively.
Find the area of a sector of a circle having radius 6 cm and length of the arc 15 cm.
In figure, a square is inscribed in a circle of diameter d and another square is circumscribing the circle. Is the area of the outer square four times the area of the inner square? Give reasons for your answer.
Find the area of the sector of a circle of radius 5 cm, if the corresponding arc length is 3.5 cm.
The number of revolutions made by a circular wheel of radius 0.25 m in rolling a distance of 11 km is ______.
