Advertisements
Advertisements
प्रश्न
A cow is tied with a rope of length 14 m at the corner of a rectangular field of dimensions 20 m × 16 m. Find the area of the field in which the cow can graze.
उत्तर
Let ABCD be a rectangular field.
Length of field = 20 m
Breadth of the field = 16 m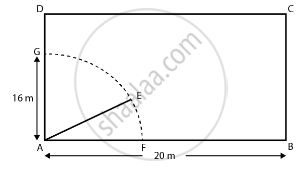
According to the question,
A cow is tied at a point A.
Let length of rope be AE = 14 m = l.
Angle subtended at the center of the sector = 90°
Angle subtended at the center (in radians) θ = `(90π)/180 = π/2`
∴ Area of a sector of a circle = `1/2 "r"^2θ`
= `1/2 xx (14)^2 xx (π/2)`
= 154 m2
Hence, the required area of a sector of a circle is 154 m2.
संबंधित प्रश्न
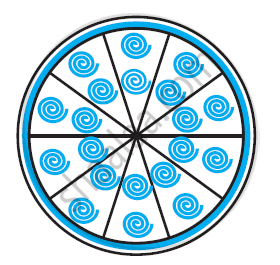
A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in figure. Find.
- The total length of the silver wire required.
- The area of each sector of the brooch [Use π = `22/7`]
The area of sector of circle of radius 2cm is 𝜋cm2. Find the angle contained by the sector.
AB is a chord of circle with centre O and radius 4cm. AB is length of 4cm. Find the area of sector of the circle formed by chord AB
A chord AB of circle, of radius 14cm makes an angle of 60° at the centre. Find the area of minor segment of circle.

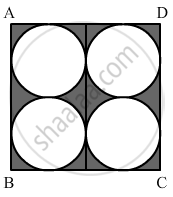
In the given figure, find the area of the shaded region, where ABCD is a square of side 14 cm and all circles are of the same diameter.
The radius of a circle with centre O is 7 cm. Two radii OA and OB are drawn at right angles to each other. Find the areas of minor and major segments.
A car has two wipers that do not overlap. Each wiper has a blade of length 21 cm sweeping through an angle of 120°. Find the total area cleaned at each sweep of the blades. `("Take" π =22/7)`
The areas of two sectors of two different circles are equal. Is it necessary that their corresponding arc lengths are equal? Why?
The length of the minute hand of a clock is 6 cm. Find the area swept by it when it moves from 7:05 p.m. to 7:40 p.m.
