Advertisements
Advertisements
प्रश्न
A car has two wipers that do not overlap. Each wiper has a blade of length 21 cm sweeping through an angle of 120°. Find the total area cleaned at each sweep of the blades. `("Take" π =22/7)`
उत्तर
Radius = r = 21 cm
sweeping angle = 120°
Total area cleaned by two wipers `= 2 xx "area cleaned by one wiper"`
Total area cleaned by two wipers `= 2 xx "area of sector with" 120^@`
`= 2 xx theta /360 xx pi"r"^2`
On substituting the values `= 2 xx 120/360 xx 22/7 xx (21)^2`
`= 2 xx 120/360 xx 22/7 xx 441`
`= (2 xx 22 xx 147)/7`
`= 6468/7 = 924`
Therefore, the area cleaned by both wipers is 924 cm2.
APPEARS IN
संबंधित प्रश्न
A car has two wipers which do not overlap. Each wiper has blade of length 25 cm sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades [Use π = `22/7`]
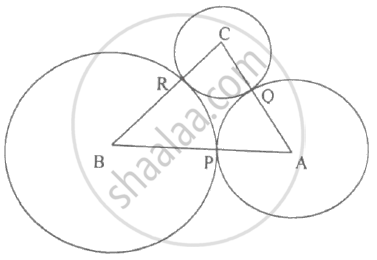
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.
The area of sector of circle of radius 2cm is 𝜋cm2. Find the angle contained by the sector.
A sector is cut-off from a circle of radius 21 cm the angle of sector is 120°. Find the length of its arc and its area.
In fig. 6, AB is a chord of a circle, with centre O, such that AB = 16 cm and radius of circle is 10 cm. Tangents at A and B intersect each other at P. Find the length of PA ?

A chord PQ of a circle with a radius of cm subtends an angle of 60° with the center of the circle. Find the area of the minor as well as the major segment. ( \[\pi\] = 3.14, \[\sqrt{3}\] = 1.73)
A chord 10 cm long is drawn in a circle whose radius is `5sqrt(2)` cm. Find the areas of both the segments.
If angle of sector is 60°, radius is 3.5 cm then length of the arc is ____________.
If `theta` is the angle in degrees of a sector of a circle of radius V, then area of the sector is ____________.
Find the difference of the areas of two segments of a circle formed by a chord of length 5 cm subtending an angle of 90° at the centre.
