Advertisements
Advertisements
प्रश्न
A chord PQ of a circle with a radius of cm subtends an angle of 60° with the center of the circle. Find the area of the minor as well as the major segment. ( \[\pi\] = 3.14, \[\sqrt{3}\] = 1.73)
उत्तर
The radius of the circle, r = 15 cm
Let O be the center and PQ be the chord of the circle.

∠POQ = θ = 60º
Area of the minor segment = Area of the shaded region
\[= r^2 \left( \frac{\pi\theta}{360°} - \frac{\sin\theta}{2} \right)\]
\[ = \left( 15 \right)^2 \times \left( \frac{3 . 14 \times 60° }{360° } - \frac{\sin60° }{2} \right)\]
\[ = 225 \times \frac{3 . 14}{6} - 225 \times \frac{\sqrt{3}}{4}\]
\[ = 117 . 75 - 97 . 31\]
\[ = 20 . 44 {cm}^2\]
Now,
Area of the circle =
Thus, the areas of the minor segment and major segment are 20.44 cm2 and 686.06 cm2, respectively.
संबंधित प्रश्न
Find the area of a quadrant of a circle whose circumference is 22 cm. [Use `pi = 22/7`]
To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships warned. [Use π = 3.14]
The perimeter of a sector of circle of radius 5.7m is 27.2 m. Find the area of sector.
The diagram shows a sector of circle of radius ‘r’ can containing an angle 𝜃. The area of sector is A cm2 and perimeter of sector is 50 cm. Prove that
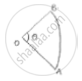
(i) 𝜃 =`360/pi(25/r− 1)`
(ii) A = 25r – r2
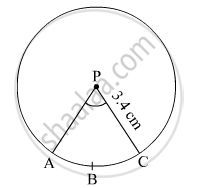
In the given figure, radius of circle is 3.4 cm and perimeter of sector P-ABC is 12.8 cm . Find A(P-ABC).
In the given figure, if O is the center of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of the shaded region is 114 cm2, find the radius of the circle. \[\pi\] = 3.14)

Area of a sector of central angle 200° of a circle is 770 cm2. Find the length of the corresponding arc of this sector.
In the given figure, ABCD is a square of side 7 cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.

A chord 10 cm long is drawn in a circle whose radius is `5sqrt(2)` cm. Find the areas of both the segments.
If angle of sector is 60°, radius is 3.5 cm then length of the arc is ____________.
The number of revolutions made by a circular wheel of radius 0.7m in rolling a distance of 176m is ______.
The areas of two sectors of two different circles are equal. Is it necessary that their corresponding arc lengths are equal? Why?
In figure, arcs are drawn by taking vertices A, B and C of an equilateral triangle of side 10 cm. to intersect the sides BC, CA and AB at their respective mid-points D, E and F. Find the area of the shaded region (Use π = 3.14).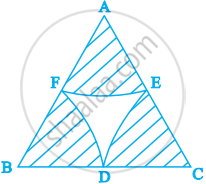
A piece of wire 20 cm long is bent into the form of an arc of a circle subtending an angle of 60° at its centre. Find the radius of the circle.
Sides of a triangular field are 15 m, 16 m and 17 m. With the three corners of the field a cow, a buffalo and a horse are tied separately with ropes of length 7 m each to graze in the field. Find the area of the field which cannot be grazed by the three animals.
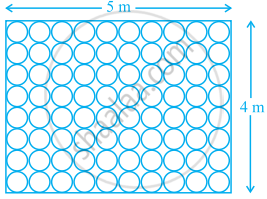
Floor of a room is of dimensions 5 m × 4 m and it is covered with circular tiles of diameters 50 cm each as shown in figure. Find the area of floor that remains uncovered with tiles. (Use π = 3.14)
Find the difference of the areas of two segments of a circle formed by a chord of length 5 cm subtending an angle of 90° at the centre.
Find the difference of the areas of a sector of angle 120° and its corresponding major sector of a circle of radius 21 cm.
Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14)
Given: The radius of a circle (r) = `square`
Measure of an arc of the circle (θ) = `square`
Area of the sector = `θ/360^circ xx square`
= `square/360^circ xx square xx square xx square`
= `square xx square xx square`
= 47.10 cm2
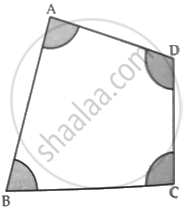
In the given figure, arcs have been drawn of radius 7 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.