Advertisements
Advertisements
प्रश्न
विकल्प
\[14\pi\]
\[\frac{7}{\pi}\]
7\[\pi\]
\[\frac{14}{\pi}\]
उत्तर
Let r be the radius of the circle.
Circumference of the circle : Area of the circle = 2 : 7
\[\Rightarrow \frac{2\pi r}{\pi r^2} = \frac{2}{7}\]
\[ \Rightarrow \frac{1}{r} = \frac{1}{7}\]
\[ \Rightarrow r = 7\]
∴ Circumference of the circle = \[2\pi r = 2\pi \times 7 = 14\pi\]
APPEARS IN
संबंधित प्रश्न
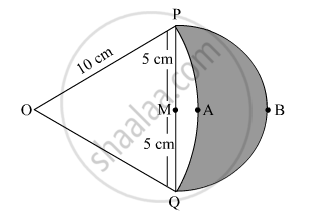
In Fig. 7, are shown two arcs PAQ and PBQ. Arc PAQ is a part of circle with centre O and radius OP while arc PBQ is a semi-circle drawn on PQ ad diameter with centre M. If OP = PQ = 10 cm show that area of shaded region is `25(sqrt3-pi/6)cm^2`.
A car has wheels which are 80 cm in diameter. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour ?
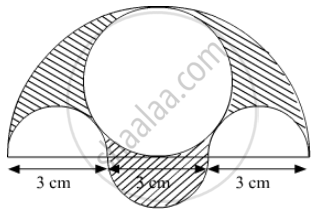
Three semicircles each of diameter 3 cm, a circle of diameter 4.5 cm and a semicircle of radius 4.5 cm are drawn in the given figure. Find the area of the shaded region
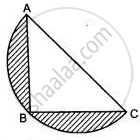
ABC is an isosceles right-angled triangle with ∠ABC = 90°. A semi-circle is drawn with AC as the diameter. If AB = BC = 7 cm, find the area of the shaded region. [Take π = 22/7]
Find the angle subtended at the centre of circle of radius ‘a’ cm by an arc of length
`(api)/4` 𝑐𝑚
In circle of radius 6cm, chord of length 10 cm makes an angle of 110° at the centre of circle find The area of sector
Below fig shows a sector of a circle, centre O. containing an angle 𝜃°. Prove that Perimeter of shaded region is 𝑟 (tan 𝜃 + sec 𝜃 +`(pitheta)/180`− 1)
The radii of two circles are 19 cm and 9 cm, Find the radius of the circle which has circumference equal to the sum of the circumferences of the two circles.
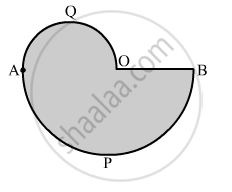
In the given figure, APB and AQO are semicircles and AO = OB. If the perimeter of the figure is 40 cm, find the area of the shaded region.
The length of a chain used as the boundary of a semicircular park is 108 m. Find the area of the park.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. The length of the arc is
The circumference of a circle is 22 cm. Find its area.
A canvas tent is in the shape of a cylinder surmounted by a conical roof. The common diameter of the cone and the cylinder is 14 m. The height of the cylindrical part is 8 m and the height of the conical roof is 4 m. Find the area of the canvas used to make the tent.
The base circumferences of two cones are the same. If their slant heights are in the ratio 5 : 4, find the ratio of their curved surface areas.
The radii of two circles are 25 cm and 18 cm. Find the radius of the circle which has a circumference equal to the sum of circumferences of these two circles.
In the given figure, the area of the shaded portion is 770 cm2. If the circumference of the outer circle is 132 cm, find the width of the shaded portion.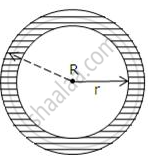
There are two circular gardens A and B. The circumference of garden A is 1.760 km and the area of garden B is 25 times the area of garden A. Find the circumference of garden B.
The radius of a circular garden is 56 m. What would it cost to put a 4-round fence around this garden at a rate of 40 rupees per metre?
A wire is bent to form a square of side 22 cm. If the wire is rebent to form a circle, its radius is ______.
